上海市浦东新区多校联考2021-2022学年七年级上学期期末质量检测数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{2} + a = a^{3}$ B、 $a^{2} \cdot a^{4} = a^{6}$ C、 ${(a^{3})}^{2} = a^{5}$ D、 $(2 a)^{2} = 2 a^{2}$

查看试题解析
2. 下列等式中，从左到右的变形是因式分解的是（）

A、 $x^{2} - 3 x - 1 = x (x - 3) - 1$ B、 $(x + y)^{2} = x^{2} + 2 x y + y^{2}$ C、 $a^{2} - a b + a = a (a - b)$ D、 $x^{2} - 9 y^{2} = (3 y + x) (x - 3 y)$

查看试题解析
3. 下列约分正确的是（）

A、 $\frac{x^{6}}{x^{2}} = x^{3}$ B、 $\frac{x^{2} + y^{2}}{x + y} = x + y$ C、 $\frac{x + m}{y + m} = \frac{x}{y}$ D、 $\frac{15 b - 5 a}{2 a - 6 b} = - \frac{5}{2}$

查看试题解析
4. 下列说法正确的是（）

A、若A、B表示两个不同的整式，则 $\frac{A}{B}$ 一定是分式 B、如果将分式 $\frac{x y}{x + y}$ 中的x和y都扩大到原来的3倍，那么分式的值不变 C、单项式 $2^{3} a b$ 是5次单项式 D、若 $3^{m} = 5 ， 3^{n} = 4$ ，则 $3^{m - n} = \frac{5}{4}$

查看试题解析
5. 多项式x²+A+1是个完全平方式，那么代数式A不可能为（）

A、2x B、x C、﹣2x D、 $\frac{1}{4}$ x⁴

查看试题解析
6. 图2是由图1经过某一种图形的运动得到的，这种图形的运动是（）

A、平移 B、翻折 C、旋转 D、以上三种都不对

查看试题解析

二、填空题

7. 电脑原价a元的八五折再减50元后的售价为元．

查看试题解析
8. 如果 $x^{3} y^{m}$ 与 $- 4 x^{- n} y$ 是同类项，那么 $n^{2} - m =$ .

查看试题解析
9. 乘积 $(x + 5) (x - 2)$ 的计算结果是．

查看试题解析
10. 计算： $(18 x^{3} y^{2} - 12 x^{2} y^{3} + x^{2} y^{2}) \div (- 6 x^{2} y^{2}) =$ .

查看试题解析
11. 因式分解： $x^{2} - 4 x - 12 =$ ．

查看试题解析
12. 对于分式 $\frac{x + y}{x - 2 y}$ ，如果 $y = 1$ ，那么x的取值范围是．

查看试题解析
13. 计算： $\frac{x^{2}}{x - y} + \frac{y^{2}}{y - x}$ = ．

查看试题解析
14. 将代数式 $\frac{y^{- 2}}{5 x^{- 1}}$ 化为只含有正整数指数幂的形式

查看试题解析
15. 如果关于 $x$ 的方程 $\frac{1}{x - 3} = 3 - \frac{k}{3 - x}$ 有增根，那么 $k =$ .

查看试题解析
16. 新型冠状病毒外包膜直径最大约140纳米（1纳米 $= 0.000001$ 毫米）．用科学记数法表示其最大直径为毫米．

查看试题解析
17. 如图，将△ABC绕着点A顺时针旋转后得到△ADE，且∠BAE=58°，则旋转角的大小是.

查看试题解析
18. 如图，长方形ABCD中，长BC=a，宽AB=b，（b＜a＜2b），四边形ABEH和四边形ECGF都是正方形．当a、b满足的等量关系是时，图形是一个轴对称图形．

查看试题解析

三、解答题

19. 计算： ${(- 2)}^{2} + {(3.14 - π)}^{0} - | - 1 | + {(\frac{1}{3})}^{- 1}$ .

查看试题解析
20. 计算： $(3 x - 2 y - 1) (3 x + 2 y - 1)$ ．

查看试题解析
21. 分解因式： $- 3 x^{3} - 3 x y^{2} - 6 x^{2} y$ ．

查看试题解析
22. 分解因式： $x y^{2} - x - y^{2} + 1$ ．

查看试题解析
23. 化简： $\frac{x^{2}}{x^{2} - 4 x + 4} \div \frac{x}{x - 2} - \frac{x - 1}{x - 2}$ ．

查看试题解析
24. 解方程： $1 - \frac{x}{x - 1} = \frac{2}{x + 1}$ .

查看试题解析
25. 在图示的方格纸中

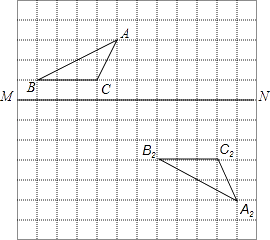(1)、作出△ABC关于MN对称的图形△A₁B₁C₁；

(2)、说明△A₂B₂C₂是由△A₁B₁C₁经过怎样的平移得到的？

查看试题解析
26. 2021年3月5日，十三届全国人大四次会议制定了2030年前碳排放达峰行动方案．为发展低碳经济、减少碳排放，于今年10月1日起上调了企业用电价格，调整后电价是调整前的1.5倍．已知某企业今年10月份比今年6月份少用电2000度，6月份的电费是4000元，10月份的电费是3600元．求：调整后每度电的价格．

查看试题解析
27. 记 $S_{n} = a_{1} + a_{2} + ⋯ + a_{n}$ ，令 $T_{n} = \frac{S_{1} + S_{2} + ⋯ + S_{n}}{n}$ ，我们称 $T_{n}$ 为这列数 $a_{1} ， a_{2} ， ⋯ ， a_{n}$ 的“理想数”．例如： $S_{1} = a_{1}$ ，则 $T_{1} = a_{1}$ ， $S_{2} = a_{1} + a_{2}$ ，则 $T_{2} = \frac{S_{1} + S_{2}}{2} = \frac{a_{1} + a_{1} + a_{2}}{2} = \frac{2 a_{1} + a_{2}}{2}$ ．

(1)、请直接写出 $T_{3} =$ ．

(2)、如果 $T_{4} = 20$ ，那么 $4 a_{1} + 3 a_{2} + 2 a_{3} + a_{4} =$ ．

(3)、已知 $a_{1} ， a_{2} ， ⋯ ， a_{500}$ 的“理想数”为2004，那么8， $a_{1} ， a_{2} ， ⋯ ， a_{500}$ 的“理想数”是多少？

查看试题解析
28. 生活中，有人喜欢把传送的便条折成“”形状，折叠过程按图①、②、③、④的顺序进行（其中阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为 $26$ 厘米，分别回答下列问题：

(1)、如果长方形纸条的宽为 $2$ 厘米，并且开始折叠时起点 $M$ 与点 $A$ 的距离为 $3$ 厘米，那么在图②中， $B E =$ 厘米；在图④中， $B M =$ 厘米．

(2)、如果长方形纸条的宽为 $x$ 厘米，现不但要折成图④的形状，而且为了美观，希望纸条两端超出点 $P$ 的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点 $M$ 与点 $A$ 的距离（结果用 $x$ 表示）．

查看试题解析