吉林省长春市长春净月高新技术产业开发区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
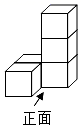
1. 2022的相反数是( )A、2022 B、-2022 C、 D、2. 2021年12月9日,“天宫课堂”第一课在中国空间站正式开讲.遍布各个测控站点的统一测控系统与架设在太空36000千米的中继卫星组网运行,提供天地之间的图象传输.请将36000用科学记数法表示为( )A、3.6×105 B、36×103 C、3.6×104 D、3.6×1033. 一个由5个相同的正方体组成的立体图形,如图所示,则这个立体图形的左视图是( )
 A、
A、 B、
B、 C、
C、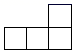 D、
D、 4. 已知代数式﹣5xyn与3xmy3是同类项,则m,n的值分别为( )A、0,3 B、1,3 C、3,0 D、3,15. 实数a、b、c、d在数轴上的对应点的位置如图所示,在这四个数中,绝对值最小的数是( )
4. 已知代数式﹣5xyn与3xmy3是同类项,则m,n的值分别为( )A、0,3 B、1,3 C、3,0 D、3,15. 实数a、b、c、d在数轴上的对应点的位置如图所示,在这四个数中,绝对值最小的数是( )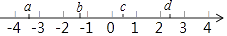 A、a B、b C、c D、d6. 如图, 是北偏东30°方向的一条射线,若射线 与射线 垂直.则 的方向角是( )
A、a B、b C、c D、d6. 如图, 是北偏东30°方向的一条射线,若射线 与射线 垂直.则 的方向角是( )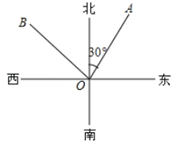 A、北偏西30° B、北偏西60° C、东偏北30° D、东偏北60°7. 如图,若要使 与 平行,则 绕点 至少旋转的度数是( )
A、北偏西30° B、北偏西60° C、东偏北30° D、东偏北60°7. 如图,若要使 与 平行,则 绕点 至少旋转的度数是( )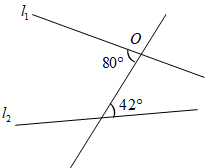 A、 B、 C、 D、8. 如图,点A是直线l外一点,过点A作AB⊥l于点B.在直线l上取一点C,连结AC,使AC=AB,点P在线段BC上,连结AP.若AB=3,则线段AP的长不可能是( )
A、 B、 C、 D、8. 如图,点A是直线l外一点,过点A作AB⊥l于点B.在直线l上取一点C,连结AC,使AC=AB,点P在线段BC上,连结AP.若AB=3,则线段AP的长不可能是( )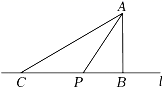 A、3.5 B、4 C、5 D、5.5
A、3.5 B、4 C、5 D、5.5二、填空题
-
9. 比较大小:﹣2 ﹣3.10. 将多项式3x2y﹣6y2+x3﹣x按x降幂排列为 .11. 若a>0,b<0,|a|>|b|,则a+b0(用“>”或“<”填空).12. 代数式x2+x+3的值为7,则代数式2x2+2x﹣3的值为 .13. 如图,EF、EG分别是∠AEB和∠BEC的平分线.若∠BEF=30°,则∠BEG=°.
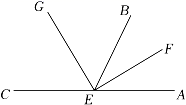 14. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
14. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
三、解答题
-
15. 计算:(1)、(﹣6)+5+(﹣2);(2)、(﹣4)×(﹣3)×(﹣25);(3)、;(4)、2×(﹣3)2﹣4÷(﹣2)﹣10.16. 先化简,再求值:(3x2﹣xy+2y2)﹣2(x2﹣xy+y2),其中x=﹣2,y= .17. 如图,已知线段AB=24cm,延长AB至C,使得BC=AB,
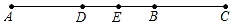 (1)、求AC的长;(2)、若D是AB的中点,E是AC的中点,求DE的长.18. “新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,实际每天生产量与计划相比有出入,把某一周的生产情况记录如下(超产为正,减产为负,单位:个):
(1)、求AC的长;(2)、若D是AB的中点,E是AC的中点,求DE的长.18. “新冠肺炎”疫情的蔓延,使得医用口罩销量大幅增加,某口罩加工厂为满足市场需求计划每天生产5000个,实际每天生产量与计划相比有出入,把某一周的生产情况记录如下(超产为正,减产为负,单位:个):星期
一
二
三
四
五
六
日
增减
+100
﹣150
+350
﹣200
+300
﹣100
+150
(1)、产量最多的一天比产量最少的一天多生产多少个?(2)、该工厂本周一共生产多少个口罩?19. 如图,已知直线l和直线外三点A、B、C,按下列要求画图:
( 1 )画射线AB;
( 2 )画线段BC;
( 3 )点E在直线l上移动,要使AE+CE最小,请先确定点E的位置,并说明你的依据是 ▲ .
20. 如图,数轴上点B表示的数为2,点B在数轴上向左移动12个单位长度到达点A,点B在数轴上向右移动4个单位长度到达点C. (1)、点A表示的数是 , 点C表示的数是 .(2)、动点P、Q同时分别从A,C出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.则点P表示的数是 ,点Q表示的数是 . (用含t的代数式表示)21. 如图,已知AEBF,AC⊥AE,BD⊥BF,AC与BD平行吗?补全下面的解答过程(理由或数学式).
(1)、点A表示的数是 , 点C表示的数是 .(2)、动点P、Q同时分别从A,C出发,点P以每秒4个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.则点P表示的数是 ,点Q表示的数是 . (用含t的代数式表示)21. 如图,已知AEBF,AC⊥AE,BD⊥BF,AC与BD平行吗?补全下面的解答过程(理由或数学式).解:∵AEBF,
∴∠EAB= ▲ . ( ▲ )
∵AC⊥AE,BD⊥BF,
∴∠EAC=90°,∠FBD=90°.
∴∠EAC=∠FBD( ▲ )
∴∠EAB﹣ ▲ =∠FBG﹣ ▲ ,
即∠1=∠2.
∴ ▲ ▲ ( ▲ ).
 22.(1)、如图1,将一副直角三角尺的直角顶点C叠放在一起,经探究发现∠ACB与∠DCE的和不变.证明过程如下:
22.(1)、如图1,将一副直角三角尺的直角顶点C叠放在一起,经探究发现∠ACB与∠DCE的和不变.证明过程如下:
由题可知∠BCE=∠ACD=90°
∴∠ACB= +∠BCD.
∴∠ACB=90°+∠BCD.
∴∠ACB+∠DCE
=90°+∠BCD+∠DCE
=90°+∠BCE
∵∠BCE=90°,
∴∠ACB+∠DCE= .
(2)、如图2,若将两个含有60°的三角尺叠放在一起,使60°锐角的顶点A重合,则∠DAB与∠CAE有怎样的数量关系,并说明理由;(3)、如图3,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的数量关系.23. 七年级地理教材第三章《天气与气候》中讲解了“气温的垂直变化”;在山地和丘陵,气温随海拔升高而降低.大致每升高100米,气温约下降0.6℃.一名同学在山脚下测得此处的海拔是720米,气温是28.8℃.(1)、若山顶的海拔是1520米,则海拔升高多少米?气温应该是多少?(2)、若山上某处的海拔是x米,请用含x的代数式表示此处的气温为℃.(3)、张老师爬到山上某处看了一下随身携带的温度计,气温为27℃,你能求出此处的海拔吗?请说明理由.24. 已知AMCN,点B在直线AM、CN之间,AB⊥BC于点B.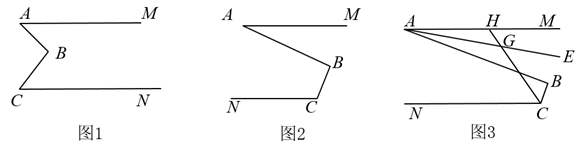 (1)、如图1,请直接写出∠A和∠C之间的数量关系: .(2)、如图2,∠A和∠C满足怎样的数量关系?请说明理由.(3)、如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .
(1)、如图1,请直接写出∠A和∠C之间的数量关系: .(2)、如图2,∠A和∠C满足怎样的数量关系?请说明理由.(3)、如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .