黑龙江省哈尔滨市香坊区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下列方程中是一元一次方程的是（  ）
    A、xy﹣2＝9 B、2y﹣1＝6 C、x+2y＝3 D、x2﹣2x+1＝0

    查看试题解析

  • 2. 下列图案中，可以利用平移来设计的图案是（  ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 在实数227 ， 2 ， π3 ， 3.14，−273中，无理数的个数是（ ）
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 4. 在如图中，∠1和∠2不是同位角的是（  ）
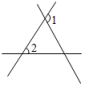    A、 B、 C、 D、

    查看试题解析

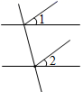  • 5. 下列等式变形中，变形的结果一定正确的是（  ）
    A、如果a＝b，那么a+3b＝5b B、如果a＝3，那么a﹣b＝3+b C、如果m＝n，那么mc＝nc D、如果mc2＝nc2 ， 那么m＝n

    查看试题解析

  • 6. 如果点P（5，y）在第四象限，则y的取值范围是（  ）
    A、y＜0 B、y＞0 C、y大于或等于0 D、y小于或等于0

    查看试题解析

  • 7. 丽宏幼儿园王阿姨给小朋友分苹果，如果每人分3个．则剩余1个；如果每人分4个，则还缺2个．问有多少个苹果？设幼儿园有x个小朋友，则可列方程为（    ）
    A、3x﹣1＝4x+2 B、3x+1＝4x﹣2 C、x+13=x−24 D、x−13=x+24

    查看试题解析

  • 8. 下列命题为假命题的是（    ）
    A、垂线段最短 B、两条直线相交，若邻补角相等，则这两条直线互相垂直 C、相等的角是对顶角 D、经过直线外一点，有且只有一条直线与这条直线平行

    查看试题解析

  • 9. 松雷商厦在某一时间以每件60元的价格售出两件衣服，其中一件盈利25%，另一件亏损25%，则售出这两件衣服总的是（  ）
    A、盈利8元 B、盈利10元 C、亏损8元 D、亏损10元

    查看试题解析

  • 10. 如图，AD∥BC，∠C＝30°，∠ADB：∠BDC＝1：2，∠EAB＝72°，以下四个说法：

    ①∠CDF＝30°；②∠ADB＝50°；

    ③∠ABD＝22°；④∠CBN＝108°

    其中正确说法的个数是（  ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 11. 5 的相反数是 ．

    查看试题解析

  • 12. 如果x＝4是关于x的方程nx﹣3＝5的解，那么n＝ ．

    查看试题解析

  • 13. 比较大小： 13 4.（填“＞”、“＜”或“＝”）

    查看试题解析

  • 14. 将命题“对顶角相等”改为“如果…那么…”的形式为：.

    查看试题解析

  • 15. 如果点P（m+3，2m﹣4）在y轴上，那么m的值是  ．

    查看试题解析

  • 16. 已知 102.01=10.1 ，则 1.0201= ．

    查看试题解析

  • 17. 如图．在2021年11月份的日历上，任意框出正方形排列的四个数a cb d ， 若这四个数的和是52，则这四个数中最大的数是  ．

    一

    二

    三

    四

    五

    六

    日

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    查看试题解析

  • 18. 如果一个正数x的平方根是2a﹣3和5﹣a，那么x的值是  ．

    查看试题解析

  • 19. 如图，在一块长20m，宽10m的长方形草地上，修建两条宽为1m的长方形小路，则这块草地的绿地面积（图中空白部分）为 m2 ．

    查看试题解析

  • 20. 如图，在数轴上，以单位长度为边长画一个正方形，点A对应的数是1，以点A为圆心，正方形对角线AB为半径画圆，圆与数轴的交点对应的数是  ．

    查看试题解析

三、解答题

  • 21. 计算：
    (1)、4+−13−19；
    (2)、33−|3−2| ．

    查看试题解析

  • 22. 解方程
    (1)、3x+6＝5（x﹣2）；
    (2)、3x+12−2=3x−14 ．

    查看试题解析

  • 23. 如图所示的方格纸中，每个小正方形的边长都是1个单位长度，三角形ABC的三个顶点都在小正方形的顶点上．

    (1)、画出三角形ABC向左平移4个单位长度后的三角形DEF（点D、E、F与点A、B、C对应），并画出以点E为原点，DE所在直线为x轴，EF所在直线为y轴的平面直角坐标系；
    (2)、在（1）的条件下，点D坐标（﹣3，0），将三角形DEF三个顶点的横坐标都减去2，纵坐标都加上3，分别得到点P、Q、M（点P、Q、M与点D、E、F对应），画出三角形PQM，并直接写出点P的坐标．

    查看试题解析

  • 24. 已知，直线AB、CD交于点O，EO⊥AB，∠EOC：∠BOD＝7：11．

    (1)、如图1，求∠DOE的度数；
    (2)、如图2，过点O画出直线CD的垂线MN，请直接写出图中所有度数为125°的角．

    查看试题解析

  • 25. 王庄去年种植“1号”油菜，今年种植“2号”油菜．“1号”油菜平均每公顷产油菜籽2400千克，“2号”油菜平均每公顷产油菜籽2700千克，今年油菜种植的面积比去年减少了3公顷，今年油菜籽的产量比去年减少了2100千克．
    (1)、求去年种植“1号”油菜的面积是多少公顷？
    (2)、求去年所产的“1号”油菜籽和今年所产的“2号”油菜籽的产量各是多少千克？
    (3)、已知“2号”油菜籽每千克的出油率比“1号”油菜籽每千克的出油提高了10%，今年油菜籽的总产油量比去年多了3750千克，求“1号”油菜籽每千克的出油率是多少？

    查看试题解析

  • 26. 已知：直线AB、CR被直线UV所截，直线UV交直线AB于点B，交直线CR于点D，∠ABU+∠CDV＝180°．

    (1)、如图1，求证：AB∥CD；
    (2)、如图2，BE∥DF，∠MEB＝∠ABE+5°，∠FDR＝35°，求∠MEB的度数；
    (3)、如图3，在（2）的条件下，点N在直线AB上，分别连接EN、ED，MG∥EN，连接ME，∠GME＝∠GEM，∠EBD＝2∠NEG，EB平分∠DEN，MH⊥UV于点H，若∠EDC＝17∠CDB，求∠GMH的度数．

    查看试题解析

  • 27. 在平面直角坐标系中，点A（m，0），点B（0，n），m=273−25 ， n−4=0 ， 将三角形BOA沿x轴向右平移8个单位长度得到三角形CDE，连接BD．

    (1)、如图1，分别求点C、D的坐标；
    (2)、如图2，点F为线段OB上一点，连接AF、CF，三角形ABF与三角形COF面积的和为10，求BF的长；
    (3)、如图3，在（2）的条件下，GH⊥OC，GH＝2，PM＝PN，线段MN自点A出发沿x轴匀速向右平移，同时点Q自点C出发以相同速度沿x轴向左平移．MN平移的过程中，点N自点A出发至点M与点H重合时，MN平移所用时间是72s．点N与点H重合至点M与点H重合时，MN平移所用时间是32s，当点Q与点P距离为6.5个单位长度时均停止运动（点P在点Q的右侧），此时直线MG交y轴于点T，求点T的坐标．

    查看试题解析