黑龙江省大庆市肇源县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. x²·x³的结果是（）

A、2x⁵ B、x⁵ C、x⁶ D、x⁸

查看试题解析
2. 下列选项中的几个图形是国际通用的交通标志，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 清代·袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来.苔花如米小，也学牡丹开.”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为（）

A、8.4×10^-5 B、8.4×10^-6 C、84×10^-7 D、8.4×10⁶

查看试题解析
4. 下列各式中，能用平方差公式计算的是（）

A、（a+b）（﹣a﹣b） B、（a+b）（a﹣b） C、（a+b）（a﹣d） D、（a+b）（2a﹣b）

查看试题解析
5. 小颖现已存款200元，为赞助“希望工程”，她计划今后每月存款10元，则存款总金额y（元）与时间x（月）之间的函数关系式是（）

A、y＝10x B、y＝120x C、y＝200－10x D、y＝200＋10x

查看试题解析
6. 转动下列各转盘，指针指向红色区域的概率最大的是（）

A、 B、 C、 D、

查看试题解析
7. 已知：如图，D、E分别在AB、AC上，若AB＝AC，AD＝AE，∠A＝60°，∠B＝25°，则∠BDC的度数是（）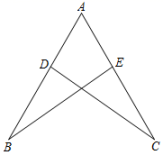

A、95° B、90° C、85° D、80°

查看试题解析
8. 如图，下列能判定 $A B / / C D$ 的条件有（）个．
（1） $∠ B + ∠ B C D = 180 °$ ；（2） $∠ 1 = ∠ 2$ ；（3） $∠ 3 = ∠ 4$ ；（4） $∠ B = ∠ 5$ ．

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，AD和BC相交于O点，OA=OC ，用“SAS”证明△AOB≌△COD还需（）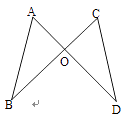

A、AB=CD B、OB=OD C、∠A=∠C D、∠AOB=∠COD

查看试题解析
10. 如图，在△ABC中， AB的垂直平分线交BC于D，AC的中垂线交BC于E，∠BAC=124°，则∠DAE的度数为（）

A、68° B、62° C、66° D、56°

查看试题解析

二、填空题

11. 填空：（a³）⁴＝．

查看试题解析
12. 在单词 $m a t h e m a t i c s$ （数学）中任意选择一个字母，选中字母“a”的概率为．

查看试题解析
13. 如图，在Rt△ABC中，∠A＝90°，∠ABC的平分线BD交AC于点D，AD＝2，BC＝6，则△BDC的面积是．

查看试题解析
14. 河北给武汉运送抗疫物资，某汽车油箱内剩余油量Q（升）与汽车行驶路程s（千米）有如下关系：
行驶路程s（千米）
0
50
100
150
200
…
剩余油量Q（升）
40
35
30
25
20
…
则该汽车每行驶100千米的耗油量为升．

查看试题解析
15. 如图， $D E / / B C$ ， $C D$ 平分 $∠ A C B$ ， $∠ A C B = 58 °$ ，则 $∠ E D C =$ ．

查看试题解析
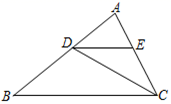16. 若一个等腰三角形的两边长分别为6和10，则这个三角形的周长.

查看试题解析
17. 如果多项式x²+（m+1）x+16是一个完全平方式，则m的值是．

查看试题解析
18. 如图，∠AOB内一点P，P₁、P₂分别是点P关于OA、OB的对称点，P₁P₂交OA于M，交OB于N，若P₁P₂＝5cm，则△PMN的周长是．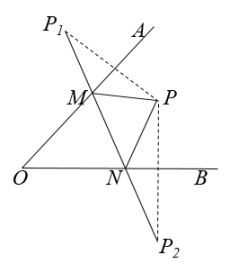

查看试题解析

三、解答题

19. 先化简，再求值：（3x+2）（3x﹣2）﹣5x（x﹣1）﹣（2x+1）² ，其中x=﹣3．

查看试题解析
20.

(1)、如图1所示，若大正方形的边长为 $a$ ，小正方形的边长为 $b$ ，则阴影部分的面积是；若将图1中的阴影部分裁剪下来，重新拼成如图2所示的一个长方形，则它的面积是；

(2)、由（1）可以得到一个乘法公式是；

(3)、利用你得到的公式计算： $202 1^{2} - 2022 \times 2020$ ．

查看试题解析
21. 已知a^x•a^y＝a⁵ ， a^x÷a^y＝a．

(1)、求x+y和x﹣y的值；

(2)、运用完全平方公式，求x²+y²的值．

查看试题解析

22. 科学家研究发现，声音在空气中传播的速度y（米/秒）与气温x（℃）之间有关，它们之间的关系如表所示：

气温/℃	…	0	5	10	15	20	…
速度/（米/秒）	…	331	334	337	340	343	…

(1)、上表中，自变量是，因变量是；

(2)、气温每上升5℃，声音在空气中的速度就增加米/秒；

(3)、直接写出y与x的关系式：；

(4)、当声音在空气中传播的速度为403米/秒时，气温x＝℃.

查看试题解析

23. 完成下面的证明
如图，点B在AG上，AG $∥$ CD，CF平分∠BCD，∠ABE＝∠FCB，BE⊥AF点E．
求证：∠F＝90°．
证明：∵AG $∥$ CD（已知）
∴∠ABC＝∠BCD（                  ▲                  ）
∵∠ABE＝∠FCB（已知）
∴∠ABC﹣∠ABE＝∠BCD﹣∠FCB
即∠EBC＝∠FCD
∵CF平分∠BCD（已知）
∴∠BCF＝∠FCD（                  ▲                  ）
∴                  ▲                  ＝∠BCF（等量代换）
∴BE $∥$ CF（                  ▲                  ）
∴                  ▲                  ＝∠F（                  ▲                  ）
∵BE⊥AF（已知）
∴                  ▲                  ＝90°（                  ▲                  ）
∴∠F＝90°．

查看试题解析
24. 如图，AC是∠BAE的平分线，点D是线段AC上的一点，∠C＝∠E，AB＝AD.求证：BC＝DE.

查看试题解析
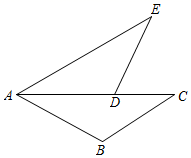25. 某商场举行有奖销售，发行奖券5万张，其中设一等奖2个、二等奖8个、三等奖40个、四等奖200个、五等奖1000个．有一位顾客购物后得到一张奖券，问这位顾客：

(1)、获得一等奖的概率是多少？

(2)、获奖的概率是多少？

查看试题解析
26. 如图，在△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，交AB于点E，连接BD．若AE＝6，△CBD的周长为20，求BC的长．

查看试题解析
27. 如图，点D为锐角∠ABC的平分线上一点，点M在边BA上，点N在边BC上，∠BMD+∠BND＝180°．试说明：DM＝DN．

查看试题解析
28. 王强同学用10块高度都是 $2 c m$ 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（ $A C = B C ， ∠ A C B = 90 °$ ），点 $C$ 在 $D E$ 上，点 $A$ 和 $B$ 分别与木墙的顶端重合.

(1)、求证： $Δ A D C ≅ Δ C E B$ ；

(2)、求两堵木墙之间的距离.

查看试题解析

行驶路程s（千米）	0	50	100	150	200	…
剩余油量Q（升）	40	35	30	25	20	…