河北省承德市承德县2021-2022学年七年级上学期期末考试数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 如果气温升高2℃时气温变化记作+2℃,那么气温下降4℃时气温变化记作( )A、+4℃ B、﹣4℃ C、+6℃ D、﹣6℃2. 下列四个算式中,有一个算式与其他三个算式的计算结果不同,该算式是( )A、 B、 C、 D、3. 在下列各式中,与 是同类项的是( )A、 ; B、 ; C、 ; D、 .4.
如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
 A、因为它最直 B、两点确定一条直线 C、两点间的距离的概念 D、两点之间,线段最短5. 下列计算正确的是( )A、 B、 C、 D、6. 若3x=4y(y≠0),则( )A、3x+4y=0 B、= C、3x+y=4y+x D、6x﹣8y=07. 下列说法中正确的是( )A、如果 ,那么x一定是7 B、 表示的数一定是负数 C、射线AB和射线BA是同一条射线 D、一个锐角的补角比这个角的余角大90°8. 一个两位数,个位数字为a,十位数比个位数字小1,则这个两位数可表示为( )A、 B、 C、 D、9. 如图,在方格纸中,将绕点按顺时针方向旋转90°后得到 , 则下列四个图形中正确的是( )
A、因为它最直 B、两点确定一条直线 C、两点间的距离的概念 D、两点之间,线段最短5. 下列计算正确的是( )A、 B、 C、 D、6. 若3x=4y(y≠0),则( )A、3x+4y=0 B、= C、3x+y=4y+x D、6x﹣8y=07. 下列说法中正确的是( )A、如果 ,那么x一定是7 B、 表示的数一定是负数 C、射线AB和射线BA是同一条射线 D、一个锐角的补角比这个角的余角大90°8. 一个两位数,个位数字为a,十位数比个位数字小1,则这个两位数可表示为( )A、 B、 C、 D、9. 如图,在方格纸中,将绕点按顺时针方向旋转90°后得到 , 则下列四个图形中正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,已知数轴上 两点表示的数分别是 ,则计算 正确的是( )
10. 如图,已知数轴上 两点表示的数分别是 ,则计算 正确的是( )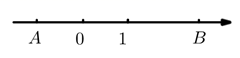 A、 B、 C、 D、11. 将一副三角板按照如图所示的位置摆放,则图中的∠α和∠β的关系一定成立的是( )
A、 B、 C、 D、11. 将一副三角板按照如图所示的位置摆放,则图中的∠α和∠β的关系一定成立的是( ) A、∠α与β互余 B、∠α与∠β互补 C、∠α与∠β相等 D、∠α比∠β小12. 当时,的值为 , 那么当时,的值为( )A、100 B、 C、98 D、13. 如图,三角形中, , . 将绕点B逆时针旋转得到 , 使点C的对应点恰好落在边上,则的度数是( )
A、∠α与β互余 B、∠α与∠β互补 C、∠α与∠β相等 D、∠α比∠β小12. 当时,的值为 , 那么当时,的值为( )A、100 B、 C、98 D、13. 如图,三角形中, , . 将绕点B逆时针旋转得到 , 使点C的对应点恰好落在边上,则的度数是( ) A、 B、 C、 D、14. 如图1是2019年4月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中错误的是( )
A、 B、 C、 D、14. 如图1是2019年4月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中错误的是( ) A、a﹣d=b﹣c B、a+c+2=b+d C、a+b+14=c+d D、a+d=b+c
A、a﹣d=b﹣c B、a+c+2=b+d C、a+b+14=c+d D、a+d=b+c二、填空题
-
15. 大于且小于的所有整数是 .16. 已知 , 则的余角是 .17. 单项式的系数是关于x的方程的解,则m的值为 .18. 观察下列等式,探究其中的规律并回答问题:
,
,
,
,
…
(1)、第4个等式中正整数k的值是;(2)、根据已知等式可归纳出第n个等式为(n是正整数).三、解答题
-
19. 计算下列各式:(1)、;(2)、;(3)、 .20.(1)、已知 , , 当 , 时,求的值;(2)、解方程: .21. 如图,已知点M在射线上,点A在直线外.
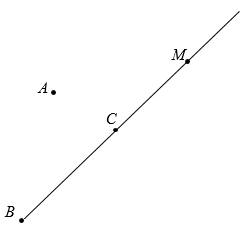
( 1 )画线段 , 连接并延长到N,使;
( 2 )在(1)的条件下用尺规作 . 且点P在线段的延长线上.(保留作图痕迹.不写作法)
22. 如图,在长方形中,点E,F分别是边 , 上一点,连接 , . 按图中各部分尺寸解决下列问题. (1)、用含x的代数式表示阴影部分的面积;(2)、当时,求阴影部分的面积.23. 如图,已知线段AB的长为a,延长线段AB至点C,使BC= .
(1)、用含x的代数式表示阴影部分的面积;(2)、当时,求阴影部分的面积.23. 如图,已知线段AB的长为a,延长线段AB至点C,使BC= . (1)、求线段AC的长(用含a的代数式表示);(2)、取线段AC的中点D,若DB=3,求a的值.24. 某县受持续干旱影响,河道水偏少,已严重影响生产和生活用水,自来水厂推行阶梯水价,引导人们节约用水,调整后的用水价格如下表:
(1)、求线段AC的长(用含a的代数式表示);(2)、取线段AC的中点D,若DB=3,求a的值.24. 某县受持续干旱影响,河道水偏少,已严重影响生产和生活用水,自来水厂推行阶梯水价,引导人们节约用水,调整后的用水价格如下表:每月用水量(吨)
单价(元/吨)
不超过20的部分
1.5
超过20不超过30的部分
2
超过30的部分
3
(1)、小明家5月份的用水量为23吨,小明家5月份的水费是元;(2)、小明家1月份水费的平均价格为每吨1.75元,求小明家1月份的用水量.25. 已知点A,B,O在一条直线上,以点O为端点在直线的同一侧作射线 , , , 使 .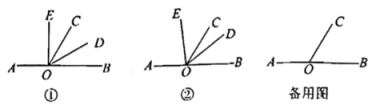 (1)、如图①,若平分 , 则的度数是;(2)、如图②,将绕点O按逆时针方向转动到某个位置,且在内部时,
(1)、如图①,若平分 , 则的度数是;(2)、如图②,将绕点O按逆时针方向转动到某个位置,且在内部时,①若 , 求的度数;
②若(n为正整数),直接用含n的代数式表示 .
26. 如图,在数轴上,点A,D表示的数分别是和15,线段 , .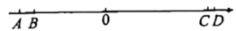 (1)、点B,C在数轴上表示的数分别是、 , 线段的长是;(2)、若线段以每秒1个单位长度的速度向右运动,同时线段以每秒2个单位长度的速度向左运动.当点B与C重合时,求这个重合点表示的数;(3)、若线段 , 分别以每秒1个单位长度利每秒2个单位长度的速度同时向左运动,设运动时间为t秒,当时,M为中点,N为中点,则线段的长为多少?
(1)、点B,C在数轴上表示的数分别是、 , 线段的长是;(2)、若线段以每秒1个单位长度的速度向右运动,同时线段以每秒2个单位长度的速度向左运动.当点B与C重合时,求这个重合点表示的数;(3)、若线段 , 分别以每秒1个单位长度利每秒2个单位长度的速度同时向左运动,设运动时间为t秒,当时,M为中点,N为中点,则线段的长为多少?