广东省广州市越秀区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 如果﹣300元表示亏本300元，那么+500元表示（）

A、亏本500元 B、盈利500元 C、亏木800元 D、盈利800元

查看试题解析
2. 如图正方体的平面展开图可知，原正方体“喜”字所在面的对面的汉字是（）

A、建 B、党 C、百 D、年

查看试题解析
3. 如图是一个正方体沿四条棱的中点切割掉一部分后的示意图，该立体图的俯视图可能是（）

A、 B、 C、 D、

查看试题解析
4. 据猫眼实时数据显示，截至2021年11月3日，电影《长津湖》累计票房正式突破55.2亿元．票房数字用科学记数法表示是（）元．

A、55.2×10⁸ B、5.52×10⁹ C、55.2×10⁹ D、5.52×10¹⁰

查看试题解析
5. 若单项式﹣10x⁹y与7x^3myⁿ是同类项，则（）

A、m＝3，n＝1 B、m＝2，n＝1 C、m＝3，n＝0 D、m＝1，n＝3

查看试题解析
6. 已知等式9a＝5b，则下列变形中不成立的是（）

A、9a﹣1＝5b﹣1 B、9ac＝5b C、9a×2＝5b×2 D、 $\frac{9 a}{2} = \frac{5 b}{2}$

查看试题解析
7. 符|﹣1|，（﹣1）² ，（﹣1）³这三个数中，等于﹣1的数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 用90立方米木料制作桌子和椅子，已知一张桌子配4张椅子，1立方米木料可做5张椅子或1张桌子，要使桌子和椅子刚好配套．设用x立方米的木料做桌子，则依题意可列方程为（）

A、4x＝5（90﹣x） B、5x＝4（90﹣x） C、x＝4（90﹣x） D、4x×5＝90﹣x

查看试题解析
9. 下列四个说法：①若a＝﹣b，则a²＝b²；②若|m|+m＝0，则m＜0；③若﹣1＜m＜0，则m²＜﹣m；④两个四次多项式的和一定是四次多项式．其中正确说法的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
10. 若关于x的一元一次方程 $\frac{3 x - 5 m}{2} - \frac{x - m}{3} = 19$ 的解，比关于x的一元一次方程﹣2（3x﹣4m）＝1﹣5（x﹣m）的解大15，则m＝（）

A、2 B、1 C、0 D、﹣1

查看试题解析

二、填空题

11. 用四舍五入法取近似数： $2.7682 \approx$ ．（精确到 $0.01$ ）

查看试题解析
12. 已知 $∠ α = 75 °$ ，则 $∠ α$ 的余角的度数为.

查看试题解析
13. 观察单项式：3a，9a² ， 27a³ ， 81a⁴…根据规律，第n个式子是．

查看试题解析
14. 两条线段，一条长10cm、另一条长12cm，将它们一端重合且放在同一条直线上，则两条线段的中点之间的距离是 cm．

查看试题解析
15. 若x^|m|﹣10＝2是关于x的一元一次方程，则m的值是．

查看试题解析
16. 当x＝2021时，ax³﹣bx+5的值为1；则当x＝﹣2021时，ax³﹣bx+5的值是．

查看试题解析

三、解答题

17. 计算：

(1)、7+（ $- \frac{1}{2}$ ）﹣3﹣（﹣1.5）

(2)、﹣2³×5﹣（﹣20）÷（﹣4）．

查看试题解析
18. 如图，在平面内有 $A ， B ， C$ 三点．

(1)、画直线 $A B$ ；画射线 $A C$ ；画线段 $B C$ ；

(2)、在线段 $B C$ 上任取一点 $D$ （不同于 $B ， C$ ），连接 $A D$ ，并延长 $A D$ 至点 $E$ ，使 $D E = A D$ ；

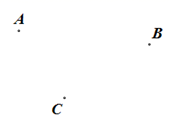(3)、数一数，此时图中共有多少条线段？多少条射线？

查看试题解析
19. 解下列方程：

(1)、5（x+8）＝3（x-2）；

(2)、 $1 - \frac{3 y - 11}{4} = \frac{7 - y}{2}$ ．

查看试题解析
20. 先化简下列各式，再求值：

(1)、（3x²y﹣4xy²）﹣（2x²y﹣3x²），其中x＝1，y＝﹣1；

(2)、3（x+y）²﹣5（x+y）+7（x+y）²+4（x+y），其中x+y＝﹣1．

查看试题解析
21. “广交会”是中国历史最长的综合性同际贸易盛会．在“广交会”中，某到会采购商计划从厂家购进甲、乙两种商品．已知甲种商品的每件进价比乙种商品的每件进价少20元．若购进甲种商品5件，乙种商品3件，共需要700元．

(1)、求甲、乙两种商品的每件进价分别是多少元？

(2)、该采购商从厂家购进了甲种商品3万件、乙种商品2万件．在销售时，甲种商品的每件售价为110元，要使得这5万件商品所获利润率为30%，求每件乙种商品的售价是多少元？

查看试题解析
22. 如图，长方形纸片ABCD，点E，F，C分别在边AD，AB，CD上．将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处．

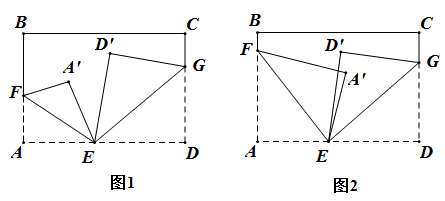(1)、如图1，若∠AEF＝40°，∠DEG＝35°，求∠A'ED'的度数；

(2)、如图1，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）；

(3)、如图2，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）．

查看试题解析
23. 如图，在数轴上点A表示的数为﹣6，点B表示的数为10，点M、N分别从原点O、点B同时出发，都向左运动，点M的速度是每秒1个单位长度，点N的速度是每秒3个单位长度，运动时间为t秒．

(1)、求点M、点N分别所对应的数（用含t的式子表示）；

(2)、若点M、点N均位于点A右侧，且AN＝2AM，求运动时间t；

(3)、若点P为线段AM的中点，点Q为线段BN的中点，点M、N在整个运动过程中，当PQ+AM＝17时，求运动时间t．

查看试题解析