北京市西城区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. -5的绝对值等于( )A、-5 B、5 C、 D、2. 云南的澄江化石地世界自然遗产博物馆升级改造完工,馆内所收藏的约520000000年前的澄江生物群化石,展示了寒武纪时期的生物多样化场景.将520000000用科学记数法表示应为( )A、 B、 C、 D、3. 如图,数轴上的点A表示的数可能是( )
 A、-4 B、-4 C、-3 D、-34. 下列计算正确的是( )A、 B、 C、 D、5. 一个角的余角比它的补角的多 , 设这个角为 , 下列关于的方程中,正确的是( )A、 B、 C、 D、6. 我国曾发行过一款如右图所示的国家重点保护野生动物(Ⅰ级)邮票小全张,设计者巧妙地将“野牦牛”和“黑颈鹤”这两枚不同规格的过桥票(无邮政铭记和面值的附票,在图中标记为①,②),与其他10枚尺寸相同的普通邮票组合在一起构成一个长方形,整个画面和谐统一,以下关于图中所示的三种规格邮票边长的数量关系的结论中,正确的是( )
A、-4 B、-4 C、-3 D、-34. 下列计算正确的是( )A、 B、 C、 D、5. 一个角的余角比它的补角的多 , 设这个角为 , 下列关于的方程中,正确的是( )A、 B、 C、 D、6. 我国曾发行过一款如右图所示的国家重点保护野生动物(Ⅰ级)邮票小全张,设计者巧妙地将“野牦牛”和“黑颈鹤”这两枚不同规格的过桥票(无邮政铭记和面值的附票,在图中标记为①,②),与其他10枚尺寸相同的普通邮票组合在一起构成一个长方形,整个画面和谐统一,以下关于图中所示的三种规格邮票边长的数量关系的结论中,正确的是( )

 A、 B、 C、 D、7. 下列方程变形中,正确的是( )A、方程 , 移项得 B、方程 , 系数化为1得 C、方程 , 去括号得 D、方程 , 去分母得8. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )
A、 B、 C、 D、7. 下列方程变形中,正确的是( )A、方程 , 移项得 B、方程 , 系数化为1得 C、方程 , 去括号得 D、方程 , 去分母得8. 用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )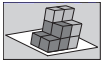 A、
A、 B、
B、 C、
C、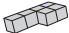 D、
D、
二、填空题
-
9. =°.10. 用四舍五入法把3.786精确到0.01,所得到的近似数为 .11. 如果单项式与是同类项,那么a= , b= .12. 若 , 则的值为 .13. 若是关于x的方程的解,则a= .14. 有理数a,b在数轴上的对应点的位置如图所示,有以下结论:①;②:③;④其中所有正确的结论是(只填写序号).
 15. 线段 , C为线段AB的中点,点D在直线AB上,若 , 则CD= .16. 在如图所示的星形图案中,十个“圆圈”中的数字分别是1,2,3,4,5,6,8,9,10,12,并且每条“直线”上的四个数字之和都相等.请将图中的数字补全 .
15. 线段 , C为线段AB的中点,点D在直线AB上,若 , 则CD= .16. 在如图所示的星形图案中,十个“圆圈”中的数字分别是1,2,3,4,5,6,8,9,10,12,并且每条“直线”上的四个数字之和都相等.请将图中的数字补全 .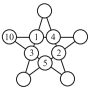
三、解答题
-
17. 计算:(1)、;(2)、(3)、(4)、18. 先化简,再求值: , 其中 .19. 平面上有三个点A,B,O.点A在点O的北偏东方向上, , 点B在点O的南偏东30°方向上, , 连接AB,点C为线段AB的中点,连接OC.(1)、依题意补全图形(借助量角器、刻度尺画图);(2)、写出的依据:(3)、比较线段OC与AC的长短并说明理由:(4)、直接写出∠AOB的度数.20. 解下列方程:(1)、;(2)、21. 如图, . , OA平分∠COE, .(1)、求∠DOE的度数(用含n的代数式表示):请将以下解答过程补充完整.

解:∵ ,
∴ .
∵ .
.
∴ ▲ . (理由: ▲ )
∵ ,
∴ .
∵OA平分∠COE,
∴∠ ▲ = . (理由: ▲ )
∴ ▲ = ▲ °.
(2)、用等式表示∠AOD与∠BOC的数量关系.22. 某班手工兴趣小组的同学们计划制作一批中国结送给敬老院作为新年礼物.如果每人制作9个,那么就比计划少做17个;如果每人制作12个,那么就比计划多做4个.(1)、这个手工兴趣小组共有多少人?计划要做的这批中国结有多少个?(2)、同学们打算用A,B两种不同的编结方式来制作这一批中国结,已知每个A型中国结需用红绳0.6米,每个B型中国结需用红绳0.9米,现有50米红绳,制作这批中国结能恰好用完这50米红绳吗?请说明你的理由.23. 在数轴上有A,B,C,M四点,点A表示的数是-1,点B表示的数是6,点M位于点B的左侧并与点B的距离是5,M为线段AC的中点. (1)、画出点M,点C,并直接写出点M,点C表示的数;(2)、画出在数轴上与点B的距离小于或等于5的点组成的图形,并描述该图形的特征;(3)、若数轴上的点Q满足 , 求点Q表示的数.24. (阅读与理解)小天同学看到如下的阅读材料:
(1)、画出点M,点C,并直接写出点M,点C表示的数;(2)、画出在数轴上与点B的距离小于或等于5的点组成的图形,并描述该图形的特征;(3)、若数轴上的点Q满足 , 求点Q表示的数.24. (阅读与理解)小天同学看到如下的阅读材料:对于一个数A,以下给出了判断数A是否为19的倍数的一种方法:
每次划掉该数的最后一位数字,将划掉这个数字的两倍与剩下的数相加得到一个和,称为一次操作,依此类推,直到数变为20以内的数为止.若最后得到的数为19.则最初的数A就是19的倍数,否则,数A就不是19的倍数.
以为例,经过第一次操作得到55,经过第二次操作得到15, , . 所以436不是19的倍数.
当数A的位数更多时,这种方法依然适用.
 (1)、(操作与说理)
(1)、(操作与说理)当时,请你帮小天写出判断过程;
(2)、小天尝试说明方法的道理,他发现解决问题的关键是每次判断过程的第一次操作,后续的操作道理都与第一次相同,于是他列出了如下表格进行分析.请你补全小天列出的表格:说明:表示 , 其中 , a,b,c均为整数.
A
A的表达式
第一次操作得到的和,记为M(A)
436
436=10×43+6
M(436)=43+2×6
532
532=
M(532)=
863
863=10×86+3
M(863)=86+2×3
……
……
……
=
M()=
(3)、利用以上信息说明:当M()是19的倍数时,也是19的倍数.25. 小冬阅读了教材中“借助三角尺画角”的探究活动(如图1、图2的实物图所示),他在老师指导下画出了图1所对应的几何图形,并标注了所使用三角尺的相应角度(如图3),他发现用一副三角尺还能画出其他特殊角.
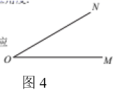
请你借助三角尺完成以下画图,并标注所使用三角尺的相应角度.
(1)、画出图2对应的几何图形;(2)、设计用一副三角尺画出角的画图方案,并画出相应的几何图形;(3)、如图4,已知 , 画∠MON的角平分线OP.26. 我们将数轴上点P表示的数记为 . 对于数轴上不同的三个点M,N,T,若有 , 其中k为有理数,则称点N是点M关于点T的“k星点”.已知在数轴上,原点为O,点A,点B表示的数分别为 . . (1)、若点B是点A关于原点O的“k星点”,则k=;若点C是点A关于点B的“2星点”,则=:(2)、若线段AB在数轴上沿正方向运动,每秒运动1个单位长度,取线段AB的中点D.是否存在某一时刻,使得点D是点A关于点O的“-2星点”?若存在,求出线段AB的运动时间;若不存在,请说明理由;(3)、点Q在数轴上运动(点Q不与A,B两点重合),作点A关于点Q的“3星点”,记为 , 作点B关于点Q的“3星点”,记为 . 当点Q运动时,是否存在最小值?若存在,求出最小值及相应点Q的位置;若不存在,请说明理由.
(1)、若点B是点A关于原点O的“k星点”,则k=;若点C是点A关于点B的“2星点”,则=:(2)、若线段AB在数轴上沿正方向运动,每秒运动1个单位长度,取线段AB的中点D.是否存在某一时刻,使得点D是点A关于点O的“-2星点”?若存在,求出线段AB的运动时间;若不存在,请说明理由;(3)、点Q在数轴上运动(点Q不与A,B两点重合),作点A关于点Q的“3星点”,记为 , 作点B关于点Q的“3星点”,记为 . 当点Q运动时,是否存在最小值?若存在,求出最小值及相应点Q的位置;若不存在,请说明理由.