北京市石景山区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、6 D、2. 北京市某周的最高平均气温是 , 最低平均气温是 , 那么这周北京市最高平均气温与最低平均气温的温差为( )A、 B、 C、 D、3. 据新京报讯,为满足节能低碳要求,石景山区总长9.6公里的“冬奥大道”照明工程全部安装LED新型高效节能电光源53000套.数字53000用科学记数法可表示为( )A、 B、 C、 D、4. 图中所示的网格是正方形网格,则下列关系正确的是( )
 A、 B、 C、 D、5. 下列几何体中,是六面体的为( )A、
A、 B、 C、 D、5. 下列几何体中,是六面体的为( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 有理数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 有理数a,b在数轴上的对应点的位置如图所示,则正确的结论是( ) A、 B、 C、 D、8. 如图,测量运动员跳远成绩选取的应是图中( )
A、 B、 C、 D、8. 如图,测量运动员跳远成绩选取的应是图中( ) A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度二、填空题
-
9. 在我们身边有很多负数,请你写出一个负数,并说明它的实际意义.这个负数是 , 它的实际意义是 .10. 若是关于x的一元一次方程的解,则a的值为 .11. 按照下面给定的计算程序,当时,输出的结果是;使代数式的值小于20的最大整数x是 .
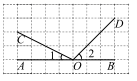
 12. 如图, , 若 , 平分 , 则的度数是 .
12. 如图, , 若 , 平分 , 则的度数是 . 13. 如图,正方形边长为 , 用含a的代数式表示图中阴影面积之和为 . (提示:横竖两条虚线将图形分成的四部分面积相等)
13. 如图,正方形边长为 , 用含a的代数式表示图中阴影面积之和为 . (提示:横竖两条虚线将图形分成的四部分面积相等) 14. 学习了一元一次方程的解法后,老师布置了这样一道题,解方程: . 小石同学的解答过程如下:
14. 学习了一元一次方程的解法后,老师布置了这样一道题,解方程: . 小石同学的解答过程如下:解方程 .
……第①步
……第②步
……第③步
……第④步
(1)、解答过程中的第①步依据是;(2)、检验是否这个方程的解,并直接写出该方程的解;15. 对于任意有理数a,b,我们规定: , 例如: .(1)、计算:;(2)、若 , 则x的值为 .16. 一组按规律排列的代数式: , 则第5个式子是 . 第2022个式子是 .三、解答题
-
17. 计算: .18. 计算: .19. 解方程: .20. 解方程: .21. 先化简,再求值: , 其中 .22. 小景准备制作一个无盖的正方体盒子.请你在图中再画出一个正方形,并将添加的正方形用阴影表示,使得新图形经过折叠后能够成为一个无盖的正方体盒子.说明:至少画出2种符合上述条件的情况.
 23. 请用下列工具按要求画图,并标出相应的字母.
23. 请用下列工具按要求画图,并标出相应的字母.已知:点P在直线a上,点Q在直线a外.
( 1 )画线段;
( 2 )画线段的中点M;
( 3 )画直线b,使于点M;
( 4 )直线b与直线a交于点N;
( 5 )利用半圆仪测量出(精确到).
 24. 列方程解应用题:某运输公司有A、B两种货车,每辆A货车比每辆B货车一次可以多运货5吨,5辆A货车与4辆B货车一次可以运货160吨.求每辆A货车和每辆B货车一次可以分别运货多少吨.
24. 列方程解应用题:某运输公司有A、B两种货车,每辆A货车比每辆B货车一次可以多运货5吨,5辆A货车与4辆B货车一次可以运货160吨.求每辆A货车和每辆B货车一次可以分别运货多少吨.

