北京市海淀区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 2022年北京冬奥会计划于2月4日开幕.作为2022年北京冬奥会雪上项目的主要举办,张家口市崇礼区建成7家大滑雪,拥有169条雪道,共162000米.数字162000用科学记数法表示为( )A、 B、 C、 D、2. 如果的相反数是1,则的值为( )A、1 B、2 C、-1 D、-23. 下列等式变形正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 关于的整式( , b,c为常数)的常数项为1,则( )A、 B、 C、 D、5. 某居民生活用水收费标准:每月用水量不超过20立方米,每立方米a元;超过部分每立方米元.该区某家庭上月用水量为25立方米,则应缴水费( )A、元 B、元 C、元 D、元6. 已知点A,B,C,D在数轴上的位置如图所示,且相邻两点之间的距离均为1个单位长度.若点A,B,C,D分别表示数 , b,c,d,且满足 , 则b的值为( )
 A、 B、 C、 D、7. 中国有悠久的金石文化,印信是金石文化的代表之一.南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印.它的表面均由正方形和等边三角形组成(如图1),可以看成图2所示的几何体.从正面看该几何体得到的平面图形是( )
A、 B、 C、 D、7. 中国有悠久的金石文化,印信是金石文化的代表之一.南北朝时期的官员独孤信的印信是迄今发现的中国古代唯一一枚楷书印.它的表面均由正方形和等边三角形组成(如图1),可以看成图2所示的几何体.从正面看该几何体得到的平面图形是( )
 A、
A、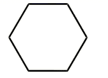 B、
B、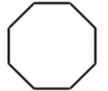 C、
C、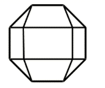 D、
D、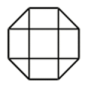
8. 几个人一起去购买物品,如果每人出8元,那么剩余3元;如果每人出7元,那么差4元.若设有x人,则下列方程中,正确的是( )A、 B、 C、 D、9. 关于x的方程的解是整数,则整数的可能值有( )A、1个 B、2个 C、3个 D、4个10. 如图,三角尺的顶点在直线上, . 现将三角尺绕点旋转,若旋转过程中顶点始终在直线的上方,设 , , 则下列说法中,正确的是( )
8. 几个人一起去购买物品,如果每人出8元,那么剩余3元;如果每人出7元,那么差4元.若设有x人,则下列方程中,正确的是( )A、 B、 C、 D、9. 关于x的方程的解是整数,则整数的可能值有( )A、1个 B、2个 C、3个 D、4个10. 如图,三角尺的顶点在直线上, . 现将三角尺绕点旋转,若旋转过程中顶点始终在直线的上方,设 , , 则下列说法中,正确的是( ) A、若 , 则 B、与一定互余 C、与有可能互补 D、若增大,则一定减小
A、若 , 则 B、与一定互余 C、与有可能互补 D、若增大,则一定减小二、填空题
-
11. 计算: .12. 关于x的方程的解是 , 则a的值是 .13. 如图所示的网格式正方形网格,∠ABC∠DEF(填“>”,“=”或“<”)
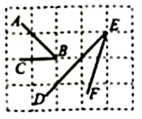 14. 已知 , 则整式的值为 .15. 某有理数满足它的绝对值等于它的相反数,写出一个符合该条件的数 .16. 如图,已知点C是线段的中点,点D是线段上的一点,若 , , 则的长度为 .
14. 已知 , 则整式的值为 .15. 某有理数满足它的绝对值等于它的相反数,写出一个符合该条件的数 .16. 如图,已知点C是线段的中点,点D是线段上的一点,若 , , 则的长度为 . 17. 如图,一艘货轮B在沿某小岛O北偏东60°方向航行中,发现了小岛O的东南方向一座灯塔A.某一时刻,灯塔A与货轮B分别到小岛O的距离恰好相等,用量角器度量得到此时的度数是°(精确到度).
17. 如图,一艘货轮B在沿某小岛O北偏东60°方向航行中,发现了小岛O的东南方向一座灯塔A.某一时刻,灯塔A与货轮B分别到小岛O的距离恰好相等,用量角器度量得到此时的度数是°(精确到度).
 18. 如图,若一个表格的行数代表关于x的整式的次数,列数代表关于x的整式的项数(规定单项式的项数为1),那么每个关于x的整式均会对应表格中的某个小方格.若关于x的整式A是三次二项式,则A对应表格中标★的小方格.已知B也是关于x的整式,下列说法正确的有 . (写出所有正确的序号)
18. 如图,若一个表格的行数代表关于x的整式的次数,列数代表关于x的整式的项数(规定单项式的项数为1),那么每个关于x的整式均会对应表格中的某个小方格.若关于x的整式A是三次二项式,则A对应表格中标★的小方格.已知B也是关于x的整式,下列说法正确的有 . (写出所有正确的序号)
①若B对应的小方格行数是4,则对应的小方格行数一定是4;
②若对应的小方格列数是5,则B对应的小方格列数一定是3;
③若B对应的小方格列数是3,且对应的小方格列数是5,则B对应的小方格行数不可能是3.
三、解答题
-
19. 计算:(1)、(2)、 .20. 解方程:(1)、(2)、 .21. 如图,已知平面上四个点A,B,C,D,请按要求完成下列问题:
 (1)、画直线 , 射线 , 连接;(2)、在线段上求作点P,使得;(保留作图痕迹)(3)、请在直线上确定一点Q,使点Q到点P与点D的距离之和最短,并写出画图的依据.22. 先化简,再求值: , 其中 , .23. 如图,点O在直线上, , , 是的平分线.
(1)、画直线 , 射线 , 连接;(2)、在线段上求作点P,使得;(保留作图痕迹)(3)、请在直线上确定一点Q,使点Q到点P与点D的距离之和最短,并写出画图的依据.22. 先化简,再求值: , 其中 , .23. 如图,点O在直线上, , , 是的平分线. (1)、若 , 求的度数;(2)、若为的平分线,求的值.24. 某校初一(3)班组织生活小常识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了其中4个参赛者的得分情况.
(1)、若 , 求的度数;(2)、若为的平分线,求的值.24. 某校初一(3)班组织生活小常识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了其中4个参赛者的得分情况.参赛者
答对题数
答错题数
得分
A
20
0
100
B
2
88
C
64
D
10
40
(1)、参赛者E说他错了10个题,得50分,请你判断可能吗?并说明理由;(2)、补全表格,并写出你的研究过程.25. 如果两个方程的解相差1,则称解较大的方程为另一个方程的“后移方程”.例如:方程是方程的后移方程.(1)、判断方程是否为方程的后移方程(填“是”或“否”);(2)、若关于x的方程是关于x的方程的后移方程,求n的值.(3)、当时,如果方程是方程的后移方程,用等式表达a,b,c满足的数量关系 .26. 在科幻世界里有各种造型奇特的小山.如图1是一座三棱锥小山,侧面展开图如图2所示,每个侧面完全相同.一只小狐狸在半山腰点M处想饱览四周风景,它沿路径“”绕小山一周最终以最短路径到达山脚A处.当小狐狸沿侧面的路径运动时,若 , 则称这段路为“上坡路”;若 , 则称这段路为“下坡路”;若 , 则称这段路为“上坡路”;若 , 则称这段路为“下坡路”.
 (1)、当时,在图2中画出从点M沿侧面环绕一周到达山脚点A处的最短路径,并判断在侧面、侧面上走的是上坡路还是下坡路?(2)、如果改变小山侧面顶角的大小,(1)中的结论是否发生变化呢?请利用量角器,刻度尺等工具画图探究,并把你的结论填入下表;
(1)、当时,在图2中画出从点M沿侧面环绕一周到达山脚点A处的最短路径,并判断在侧面、侧面上走的是上坡路还是下坡路?(2)、如果改变小山侧面顶角的大小,(1)中的结论是否发生变化呢?请利用量角器,刻度尺等工具画图探究,并把你的结论填入下表;情形
度数
侧面
侧面
1
15°
2
30°
(3)、记 , 随着逐渐增大,在侧面、侧面上走的这两段路上下坡变化的情况为 .27. 在数轴上,把原点记作点O,表示数1的点记作点A.对于数轴上任意一点P(不与点O,点A重合),将线段与线段的长度之比定义为点P的特征值,记作 . 即 . 例如:当点P是线段的中点时,因为 , 所以 . (1)、如图,点 , , 为数轴上三个点,点表示的数是 , 点与关于原点对称.
(1)、如图,点 , , 为数轴上三个点,点表示的数是 , 点与关于原点对称.
①;
②比较 , , 的大小(用“<”连接);
(2)、数轴上的点M满足 , 求;(3)、数轴上的点P表示有理数p,已知且为整数,则所有满足条件的p的倒数之和为 .