北京市房山区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 有理数5的相反数是( )A、5 B、 C、 D、2. 下列几何体中,是圆锥的为( )A、
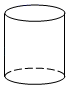 B、
B、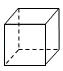 C、
C、 D、
D、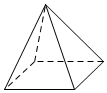 3. 袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年艰苦努力,目前我国杂交水稻种植面积达2.4亿亩,每年增产的粮食可以养活80000000人.将80000000用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 将一副直角三角板如图所示摆放,则图中的大小为( )
3. 袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年艰苦努力,目前我国杂交水稻种植面积达2.4亿亩,每年增产的粮食可以养活80000000人.将80000000用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 将一副直角三角板如图所示摆放,则图中的大小为( ) A、75° B、120° C、135° D、150°6. 单项式的系数和次数分别为( )A、-2,3 B、-2,4 C、2,3 D、2,47. 已知是关于x的方程的解,则a的值为( )A、-5 B、-3 C、3 D、58. 如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面留出宽都是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( )
A、75° B、120° C、135° D、150°6. 单项式的系数和次数分别为( )A、-2,3 B、-2,4 C、2,3 D、2,47. 已知是关于x的方程的解,则a的值为( )A、-5 B、-3 C、3 D、58. 如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面留出宽都是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( ) A、 B、 C、 D、9. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问:人数、物价各是多少?若设物价是x钱,根据题意列一元一次方程,正确的是( )
A、 B、 C、 D、9. 《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.问:人数、物价各是多少?若设物价是x钱,根据题意列一元一次方程,正确的是( ) A、 B、 C、 D、10. 有理数 , , , 在数轴上的对应点的位置如图所示.则在下列选项中,正确的是( )
A、 B、 C、 D、10. 有理数 , , , 在数轴上的对应点的位置如图所示.则在下列选项中,正确的是( )
①如果 , 则一定会有;②如果 , 则一定会有;③如果 , 则一定会有;④如果 , 则一定会有 .
A、①④ B、①③ C、②③ D、②④二、填空题
-
11. 如图是某几何体的展开图,该几何体是.
 12. 15.7°=度分.13. 比较大小: .14. 请写出一个解为2的一元一次方程,这个方程可以为 .15. 下图所示的网格是正方形网格, .(填“ ”,“ ”或“ ”)
12. 15.7°=度分.13. 比较大小: .14. 请写出一个解为2的一元一次方程,这个方程可以为 .15. 下图所示的网格是正方形网格, .(填“ ”,“ ”或“ ”) 16. 如图,在公园绿化时,需要把管道l中的水引到A,B两处.工人师傅设计了一种又快又节省材料的方案如下:
16. 如图,在公园绿化时,需要把管道l中的水引到A,B两处.工人师傅设计了一种又快又节省材料的方案如下:
画法:如图,
⑴连接AB;
⑵过点A画线段直线l于点C,所以线段AB和线段AC即为所求.

请回答:工人师傅的画图依据是 .
17. 已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,若 , , 则线段CD的长为 .18. 如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-3,-2,-1,0,且任意相邻4个台阶上数的和都相等. (1)、第5个台阶上的数x是;(2)、若第n个-2出现在第2022个台阶上,则n的值为 .
(1)、第5个台阶上的数x是;(2)、若第n个-2出现在第2022个台阶上,则n的值为 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 解方程:(1)、;(2)、 .21. 下面是小贝同学解方程的过程,请认真阅读并完成相应任务.
.
解:………………………………第一步
………………………………第二步
………………………………第三步
………………………………第四步
………………………………第五步
(1)、任务一:填空:
以上解题过程中,第一步是依据进行变形的;第二步是依据(运算律)进行变形的;(2)、第步开始出现错误,这一步的错误的原因是;(3)、任务二:请直接写出该方程的正确的解: .22. 如图,已知平面上有三个点A,B,C,请按要求画图,并回答问题:( 1 )画直线AB,射线CA;
( 2 )延长AC到D,使得 , 连接BD;
( 3 )过点B画 , 垂足为E;
( 4 )通过测量可得,点B到直线AC的距离约为 ▲ cm.(精确到0.1cm)
 23. 先化简,再求值: , 其中 .24. 列一元一次方程解应用题:国家速滑馆“冰丝带”,位于北京市朝阳区奥林匹克公园林萃路2号,是2022年北京冬奥会北京主赛区标志性、唯一新建的冰上竞赛场馆.某大学冬奥志愿者负责本场馆的对外联络和文化展示服务工作,负责对外联络服务工作的有17人,负责文化展示服务工作的有10人,现在另调20人去两服务处支援,使得在对外联络服务工作的人数比在文化展示服务的人数的2倍多5人,问应调往对外联络、文化展示两服务处各多少人?25. 已知:点O是直线AB上一点,过点O分别画射线OC,OE,使得 .(1)、如图,OD平分 . 若 , 求的度数.请补全下面的解题过程(括号中填写推理的依据).
23. 先化简,再求值: , 其中 .24. 列一元一次方程解应用题:国家速滑馆“冰丝带”,位于北京市朝阳区奥林匹克公园林萃路2号,是2022年北京冬奥会北京主赛区标志性、唯一新建的冰上竞赛场馆.某大学冬奥志愿者负责本场馆的对外联络和文化展示服务工作,负责对外联络服务工作的有17人,负责文化展示服务工作的有10人,现在另调20人去两服务处支援,使得在对外联络服务工作的人数比在文化展示服务的人数的2倍多5人,问应调往对外联络、文化展示两服务处各多少人?25. 已知:点O是直线AB上一点,过点O分别画射线OC,OE,使得 .(1)、如图,OD平分 . 若 , 求的度数.请补全下面的解题过程(括号中填写推理的依据).解:∵点O是直线AB上一点,
∴ .
∵ ,
∴ .
∵OD平分 .
∴( ▲ ).
∴ ▲ °.
∵ ,
∴( ▲ ).
∵ ▲ ▲ ,
∴ ▲ °.
 (2)、在平面内有一点D,满足 . 探究:当时,是否存在的值,使得 . 若存在,请直接写出的值;若不存在,请说明理由.26. 定义:点C在线段AB上,若点C到线段AB两个端点的距离成二倍关系时,则称点C是线段AB的闭二倍关联点.(1)、如图,若点A表示数-1,点B表示的数5,下列各数-3,1,3所对应的点分别为 , , , 则其中是线段AB的闭二倍关联点的是 ;
(2)、在平面内有一点D,满足 . 探究:当时,是否存在的值,使得 . 若存在,请直接写出的值;若不存在,请说明理由.26. 定义:点C在线段AB上,若点C到线段AB两个端点的距离成二倍关系时,则称点C是线段AB的闭二倍关联点.(1)、如图,若点A表示数-1,点B表示的数5,下列各数-3,1,3所对应的点分别为 , , , 则其中是线段AB的闭二倍关联点的是 ; (2)、若点A表示的数为-1,线段AB的闭二倍关联点C表示的数为2,则点B表示的数为;(3)、点A表示的数为1,点C,D表示的数分别是4,7,点O为数轴原点,点B为线段CD上一点.设点M表示的数为m.若点M是线段AB的闭二倍关联点,求m的取值范围.
(2)、若点A表示的数为-1,线段AB的闭二倍关联点C表示的数为2,则点B表示的数为;(3)、点A表示的数为1,点C,D表示的数分别是4,7,点O为数轴原点,点B为线段CD上一点.设点M表示的数为m.若点M是线段AB的闭二倍关联点,求m的取值范围.