北京市大兴区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. －2022的倒数是（）

A、 $- \frac{1}{2022}$ B、 $\frac{1}{2022}$ C、－2022 D、2022

查看试题解析
2. 据国家统计局公布的全国粮食生产数据显示.2021年全国粮食播种面积为117632000公顷，粮食总产量为13657亿斤，将117632000用科学记数法表示为（）

A、 $0.117632 \times 1 0^{9}$ B、 $1.17632 \times 1 0^{8}$ C、 $11.7632 \times 1 0^{7}$ D、 $117632 \times 1 0^{3}$

查看试题解析
3. 下列各组数中，互为相反数的是（）

A、 $- 2^{3}$ 与（ $- 2)^{3}$ B、－（－2）与 $| - 2 |$ C、 $- 5^{2}$ 与 $- 2^{5}$ D、 $- 3^{2}$ 与 $(- 3)^{2}$

查看试题解析
4. 有理数a，b，c在数轴上的对应点的位置如图所示，若 $| b | = | c |$ ，则下列结论错误的是（）

A、 $a + b < 0$ B、 $a + c < 0$ C、 $a b < 0$ D、 $\frac{b}{c} < 0$

查看试题解析
5. 下列说法中，正确的是（）

A、若 $a = b$ ，则 $a + 2 = b - 2$ B、若 $a = b$ ，则 $- 4 a = - 4 b$ C、若 $\frac{a}{2} = 2$ ，则 $a = 1$ D、若 $a - b - 2 = 0$ ，则 $a = b - 2$

查看试题解析
6. 钟面上，时针与分针在不停的旋转，从6时到18时，若某整点时刻的时针与分针构成的角为 $60 °$ ，则这个时刻是（）

A、10时 B、11时 C、10时或14时 D、11时或13时

查看试题解析
7. 甲、乙、丙三家商店对一种定价相同的文具开展促销活动，甲商店一次性降价30%；乙商店连续两次降价15%；丙商店先降价20%后又降价10%．若小雪准备在促销活动中，购买此种文具，则下列说法中，正确的是（）

A、小雪到甲商店购买这种文具更合算 B、小雪到乙商店购买这种文具更合算 C、小雪到丙商店购买这种文具更合算 D、在促销活动中，三家商店的这种文具售价相同，小雪可任选一家购买

查看试题解析
8. 如图所示，用火柴棍按如下规律拼图，若第①个图形需要4根火柴棍，则第⑩个图形需要的火柴棍根数为（）

A、110 B、180 C、220 D、264

查看试题解析

二、填空题

9. 若 $\frac{1}{6} x^{n + 1} y^{3}$ 与 $x^{5} y^{3}$ 是同类项，则n的值为．

查看试题解析
10. 若 $x = 3$ 是关于x的方程 $2 x + a = 5$ 的解，则a的值是．

查看试题解析
11. 将两块直角三角尺的直角顶点重合为如图的位置，若∠AOC＝20°，则∠BOD＝．

查看试题解析
12. 比较大小： $16 ° 25$ $16.25 °$ （填“＞”“＜”或“＝”）．

查看试题解析
13. 请你写出一个二次项系数为1的二次三项式．

查看试题解析
14. 如图是正方体的一种展开图，表面上的语句为北京2022年冬奥会和冬残奥会的主题口号“一起向未来！”，那么在正方体的表面与“！”相对的汉字是．

查看试题解析
15. 用一组a，b的值说明“若a，b为分数，则a与b的和一定大于a与b的差”是错误的，这组值可以是a＝， b＝．

查看试题解析
16. 《九章算术》是中国古代的数学专著，收有246个与生产、生活实践有联系的应用问题．书中有这样一个问题：今有醇酒一斗，直钱五十；行酒一斗，直钱一十．今将钱三十，得酒二斗，问醇、行酒各得几何？意思是：今有醇酒（美酒）1斗，价格是50钱；行酒（普通酒）1斗，价格是10钱．现花30钱买了2斗酒，问醇酒，行酒各买得多少斗？若设买得醇酒x斗，则可列一元一次方程为．

查看试题解析

三、解答题

17. 计算： $- 3 + (- 5) + | 1 - 8 |$

查看试题解析
18. 计算： $(\frac{1}{4} + \frac{1}{6} - \frac{2}{3}) \times (- 12)$

查看试题解析
19. 计算： ${(- 2)}^{2} \times 3 + 36 \div (- 6) \times \frac{1}{2}$

查看试题解析
20. 解方程： $3 (3 x - 1) - 4 = 17 x$

查看试题解析
21. 解方程： $\frac{2 x + 1}{3} = 1 - \frac{x + 6}{2}$

查看试题解析
22. 化简求值； $2 (a^{2} b - 3 a b - 1) - (2 a^{2} b - 5 a b)$ ．其中 $a = - 2 ， b = - \frac{1}{3}$ ．

查看试题解析
23. 按下列语句完成作图：
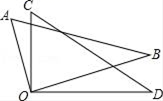
已知：如图，点A是射线OB外一点．
（ 1 ）画射线OA；
（ 2 ）在射线OB上截取OC＝OA；
（ 3 ）画∠AOC的角平分线OD；
（ 4 ）在射线OD上确定一点P，使得AP＋CP的值最小（保留作图痕迹）．

查看试题解析
24. 已知一个角的补角等于这个角的余角的4倍，求这个角的度数．

查看试题解析
25. 如图，点C为线段AB的中点，点D在线段CB上，若AD＝3cm，DB＝2cm，求CD的长．
请将下面的解题过程补充完整：
解：因为AD＝3cm，DB＝2cm．
所以                  ▲                  ＝AD＋DB＝3＋2＝5（cm）．
因为点C为线段AB的中点，所以 $A C = \frac{1}{2}$                    ▲                  ＝                  ▲                  cm．
所以CD＝                  ▲                  －                  ▲                  ＝                  ▲                  cm．

查看试题解析
26. 列一元一次方程解应用题：用A4纸在某文印社复印，复印页数不超过20时，每页收费0.12元；复印页数超过20时，超过部分每页收费降为0.09元．在某图书馆复印同样的文件，无论复印多少页，每页收费0.1元．若小华复印资料恰好花费了4.83元，请问小华是在文印社还是在图书馆复印的？复印了多少页？

查看试题解析
27. 定义一种新运算 $▽$ ：对于任意有理数x和y，有 $x ▽ y = m x - n y + x y$ （m，n为常数且 $m n \neq 0$ ），如： $2 ▽ 3 = 2 m - 3 n + 2 \times 3 = 2 m - 3 n + 6$ ．

(1)、① $\frac{1}{2} ▽ 2$ ＝ ▲ （用含有m，n的式子表示）；
②若 $\frac{1}{2} ▽ 2 = 3$ ，求1 $▽$ 4的值；

(2)、请你写出一组m，n的值，使得对于任意有理数x，y， $x ▽ y = y ▽ x$ 均成立．

查看试题解析
28. 已知 $∠ M O N = 120 °$ ， $∠ A O B = 60 °$ ， OC平分∠AON．

(1)、如图1，射线 $O A$ 与射线OB均在∠MON的内部．
①若 $∠ B O C = 20 °$ ， ∠MOA＝ ▲ °；
②若 $∠ B O C = α$ ，直接写出∠MOA的度数（用含 $α$ 的式子表示）；

(2)、如图2，射线OA在∠MON的内部，射线OB在∠MON的外部．
①若 $∠ B O C = α$ ，求∠MOA的度数（用含 $α$ 的式子表示）；
②若在∠MOA的内部有一条射线OD，使得 $∠ A O D = ∠ B O N$ ，直接写出∠MOD的度数．

查看试题解析