北京市朝阳区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 风云二号是我国自行研制的第一代地球静止气象卫星，它在地球赤道上空距地面约35800公里的轨道上运行．将35800用科学记数法表示应为（）

A、 $0.358 \times 1 0^{5}$ B、 $35.8 \times 1 0^{3}$ C、 $3.58 \times 1 0^{5}$ D、 $3.58 \times 1 0^{4}$

查看试题解析
2. 下列两个数中，互为相反数的是（）

A、＋2和－2 B、2和 $- \frac{1}{2}$ C、2和 $\frac{1}{2}$ D、＋2和 $| - 2 |$

查看试题解析
3. 若 $4 x y^{2}$ 与 $x y^{m}$ 是同类项，则m的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 下列的四个角中，是图中角的补角的是（）

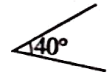A、 B、 C、 D、

查看试题解析
5. 如果a＝b，那么下列等式一定成立的是（）

A、 $a + \frac{1}{2} = b - \frac{1}{2}$ B、a＝－b C、 $\frac{a}{5} = \frac{b}{5}$ D、ab＝1

查看试题解析
6. 下列平面图形中，能折叠成棱柱的是（）

A、 B、 C、 D、

查看试题解析
7. 若方程 $x + 1 = \frac{1}{4}$ 的解是关于x的方程4x＋4＋m＝3的解，则m的值为（）

A、－4 B、－2 C、2 D、0

查看试题解析
8. 棱长为a的小正方体按照如图所示的规律摆放，从上面看第100个图，得到的平面图形的面积为（）

A、100a B、 $5050 a^{2}$ C、 $6000 a^{2}$ D、 $10100 a^{2}$

查看试题解析

二、填空题

9. 月球表面的白天平均温度为零上126℃，夜间平均温度为零下150℃．如果零上126℃记作＋126℃，那么零下150℃应该记作℃．

查看试题解析
10. 计算 $(+ 1 \frac{1}{5}) - (- \frac{2}{5}) + (- \frac{3}{5}) =$ ．

查看试题解析
11. 如图，将甲，乙两把尺子拼在一起，两端重合，如果甲尺经校定是直的，那么乙尺不是直的，判断依据是.

查看试题解析
12. 同一个式子可以表示不同的含义，例如6n可以表示长为6，宽为n的长方形面积，也可以表示更多的含义，请你给6n再赋予一个含义．

查看试题解析
13. 如图，OB，OC分别是 $∠ A O C$ ， $∠ B O D$ 的三等分线，若 $∠ A O B = 17 ° 15$ ，则 $∠ C O D$ 的度数为．

查看试题解析
14. 计算： ${(- 2)}^{3} \div 8 + {(- 1)}^{20} =$ ．

查看试题解析
15. 若一个多项式减去 $3 x^{2} - x$ 等于x－1，则这个多项式是．

查看试题解析
16. 下表是某校七年级各班某月课外兴趣小组活动时间的统计表，其中各班同一兴趣小组每次活动时间相同．

体育小组活动次数
科技小组活动次数
文艺小组活动次数
课外兴趣小组活动总时间（单位：h）
1班
4
6
5
11.5
2班
4
6
4
11
3班
4
7
4
12
4班
6
13
（说明：活动次数为正整数）
科技小组每次活动时间为h，该年级4班这个月体育小组活动次数最多是次．

查看试题解析

三、解答题

17. 下面是小明和小乐在学习有理数运算后的一段对话．
请你完成下面的运算，并填写运算过程中的依据
解：3－5
＝3＋（                  ▲            ）（依据：                  ▲            ）
＝－（                  ▲            －3）
＝                  ▲             ．

查看试题解析
18.

(1)、画出数轴，并表示下列有理数：－2， $\frac{1}{3}$ ， 1.5；

(2)、在（1）的条件下，点O表示0，点A表示－2，点B表示 $\frac{1}{3}$ ，点C表示1.5，点D表示数a，－1＜a＜0，下列结论：①AO＞DO；②BO＞DO；③CO＞DO．其中一定正确的是（只需填写结论序号）．

查看试题解析
19.

(1)、读语句，并画出图形：三条直线AB，BC，AC两两相交，在射线AB上取一点D（不与点A重合），使得BD＝AB，连接CD．

(2)、在（1）的条件下，回答问题：①用适当的语句表述点D与直线BC的关系：；
②若AB＝3，则AD＝．

查看试题解析
20. 当x为何值时，式子 $\frac{1}{5} (5 x - 1)$ 与 $\frac{1}{2} x$ 的值相等？

查看试题解析
21. 先化简，再求值： $2 a^{2} b + 3 a b^{2} - 2 (a^{2} b + a b^{2}) + a b^{2}$ ，其中 $a = \frac{1}{2}$ ， b＝－3．

查看试题解析
22. 解方程： $\frac{2 x + 1}{3} = 1 + \frac{x - 1}{2}$ ．

查看试题解析
23. 列方程解应用题
迎接2022年北京冬奥会，响应“三亿人上冰雪”的号召，全民参与冰雪运动的积极性不断提升．我国2019年总滑雪人次比2016年总滑雪人次多了约680.5万，2019年旱雪人次约占本年总滑雪人次的1.5%，比2016年总滑雪人次的2%多2.6万.2019年总滑雪人次是多少万？

查看试题解析
24. 阅读下面材料：活动1利用折纸作角平分线
①画图：在透明纸片上画出 $∠ P Q R$ （如图1-①）；②折纸：让 $∠ P Q R$ 的两边QP与QR重合，得到折痕QH（如图1-②）；③获得结论：展开纸片，QH就是 $∠ P Q R$ 的平分线（如图1-③）．
活动2利用折纸求角
如图2，纸片上的长方形ABCD，直线EF与边AB，CD分别相交于点E，F．将 $∠ A E F$ 对折，点A落在直线EF上的点 $A$ 处，折痕EN与AD的交点为N；将 $∠ B E F$ 对折，点B落在直线EF上的点 $B$ 处，折痕EM与BC的交点为M．这时 $∠ N E M$ 的度数可知，而且图中存在互余或者互补的角．

(1)、解：（1）利用活动1可知，EN是 $∠ A E A$ 的平分线，EM是 $∠ B E B$ 的平分线，所以 $∠ A E N = \frac{1}{2} ∠$ ▲ ， $∠ B E M = \frac{1}{2} ∠$ ▲ ．由题意可知， $∠ A E B$ 是平角．所以 $∠ N E M = ∠ A E N + ∠ B E M = \frac{1}{2}$ （∠ ▲ ＋∠ ▲ ）＝ ▲ °．
解答问题：求 $∠ N E M$ 的度数；

(2)、①图2中，用数字所表示的角，哪些与 $∠ A E N$ 互为余角？
②写出 $∠ A E N$ 的一个补角．

查看试题解析
25. 我们用 $\bar{x y z}$ 表示一个三位数，其中x表示百位上的数，y表示十位上的数，z表示个位上的数，即 $\bar{x y z} = 100 x + 10 y + z$ ．

(1)、说明 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 一定是111的倍数；

(2)、①写出一组a，b，c的取值，使 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 能被7整除，这组值可以是a＝， b＝， c＝；
②若 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 能被7整除，则a，b，c三个数必须满足的数量关系是．

查看试题解析
26. 对数轴上的点和线段，给出如下定义：点M是线段a的中点，点N是线段b的中点，称线段MN的长度为线段a与b的“中距离”．已知数轴上，线段AB＝2（点A在点B的左侧），EF＝6（点E在点F的左侧）．

(1)、当点A表示1时，
①若点C表示－2，点D表示－1，点H表示4，则线段AB与CD的“中距离”为3.5，线段AB与CH的“中距离”为；
②若线段AB与EF的“中距离”为2，则点E表示的数是．

(2)、线段AB、EF同时在数轴上运动，点A从表示1的点出发，点E从原点出发，线段AB的速度为每秒1个单位长度，线段EF的速度为每秒2个单位长度，开始时，线段AB，EF都向数轴正方向运动；当点E与点B重合时，线段EF随即向数轴负方向运动，AB仍然向数轴正方向运动．运动过程中，线段AB、EF的速度始终保持不变．设运动时间为t秒．
①当t＝2.5时，线段AB与EF的“中距离”为 ▲ ；
②当线段AB与EF的“中距离”恰好等于线段AB的长度时，求t的值．

查看试题解析

	体育小组活动次数	科技小组活动次数	文艺小组活动次数	课外兴趣小组活动总时间（单位：h）
1班	4	6	5	11.5
2班	4	6	4	11
3班	4	7	4	12
4班		6		13