安徽省安庆市宿松县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 2021年电影《长津湖》上映后，票房一路高歌，不断刷新纪录，10月11日单日票房为1.03亿元，1.03亿用科学记数法可表示为（）

A、10.3×10⁸ B、1.03×10⁸ C、1.03×10⁹ D、103×10⁷

查看试题解析
3. 下列计算正确的是（　　）

A、 $3 a - 2 b = a b$ B、 $5 y - 3 y = 2$ C、 $7 a + a = 7 a^{2}$ D、 $3 x^{2} y - 2 y x^{2} = x^{2} y$

查看试题解析
4. 有理数数a，b在数轴上的对应点的位置如图所示，下列结论正确的是（）

A、－a＜b B、a＋b＜0 C、－b＞ a D、a－b＞0

查看试题解析
5. 单项式 $x^{m - 1} y^{3}$ 与 $- 4 x y^{n}$ 是同类项，则 $m^{n}$ 的值是（）

A、1 B、3 C、6 D、8

查看试题解析
6. 若 $2 a = b + 1$ ， $c = 2 b$ ，则 $- 6 a + b + c$ 的值为（）

A、 $- 3$ B、3 C、 $- 4$ D、4

查看试题解析
7. 下列四个选项中，不一定成立的是（）

A、若 $x = y$ ，则 $2 x = x + y$ B、若 $2 x = 3 x + 4$ ，则 $3 x - 2 x = - 4$ C、若 $x z = y z$ ，则 $x = y$ D、若 $x = y$ ，则 $x z = y z$

查看试题解析
8. 下列说法中，正确的是（　　）
①射线AB和射线BA是同一条射线；
②若AB=BC，则点B为线段AC的中点；
③同角的补角相等；
④点C在线段AB上，M，N分别是线段AC，CB的中点．若MN=5，则线段AB=10．

A、①② B、②③ C、②④ D、③④

查看试题解析
9. 如果 $∠ α$ 和 $∠ β$ 互余，则下列式子中表示 $∠ α$ 补角是（）
①180°－ $∠ α$ ；② $∠ α$ ＋2 $∠ β$ ；③2 $∠ α$ ＋ $∠ β$ ；④ $∠ β$ ＋90°

A、①②④ B、①②③ C、①③④ D、②③④

查看试题解析
10. 把1～9这九个数填入 $3 \times 3$ 方格中，使其任意一行，任意一列及任意一条对角线上的数之和都相等，这样便构成了一个“九宫格”，它源于我国古代的“洛書”（图1），是世界上最早的“幻方”．图2是仅可以看到部分数值的“九宫格”，则 $x^{y}$ 的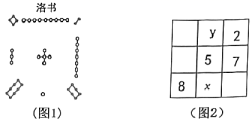值为（）

A、9 B、1 C、8 D、 $- 8$

查看试题解析

二、填空题

11. 单项式 $\frac{- 2 x^{2} y}{5}$ 的系数是，次数是。

查看试题解析
12. 计算： $- 2 \div 2 \times \frac{1}{2}$ 结果是．

查看试题解析
13. 临近春节，商场开展打折促销活动，某商品如果按原售价的八折出售，将盈利10元；如果按原售价的六折出售，将亏损50元．问该商品的原售价为多少元？设该商品的原售价为x元，则列方程为．

查看试题解析
14. 学校举办图画展览，需要依次把图画作品横着钉成一排（如图），图中黑色实心圆点表示图钉．照这样，钉30张图画需要图钉颗．

查看试题解析
15. 数轴上A、B两点对应的数分别为a、b，则A、B两点之间的距离表示为： $A B = | a - b |$ ．若数轴上A、B两点对应的数分别为a、b，且满是 $| a + 5 | + {(b - 10)}^{2} = 0$ ．

(1)、求得A、B两点之间的距离是；

(2)、若P、Q两点在数轴上运动，点P从A出发以2个单位长度/秒的速度向右匀速运动，同时，点Q从B出发以3个单位长度/秒的速度向左匀速运动．经过秒，P、Q两点相距5个单位长度．

查看试题解析

三、解答题

16.

(1)、 $26 - 17 + (- 6) - 33$

(2)、 $- 2^{4} \div {(\frac{4}{3})}^{2} \times (- \frac{1}{3}) - | - 6 - 2 |$

查看试题解析
17. 先化简，再求值：3（x²﹣xy）﹣2（x²﹣y²）+3xy，其中x＝﹣1，y＝2．

查看试题解析
18.

(1)、 $\frac{x + 1}{2} = x - 1$

(2)、 ${\begin{array}{l} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3 x + 2 y = 4 \end{array}$

查看试题解析
19. 《四元玉鉴》是一部成就辉煌的数学名著，在中国古代数学史上有着重要地位．其中.
酒分醇醨
务中听得语吟吟，言道醇醨酒二盆．
醇酒一升醉三客，醨酒三升醉一人．
共通饮了一斗九，三十三客醉醨醨．
欲问高明能算士，几何醨酒几多醇？
其大意为：有好酒和薄酒分别装在瓶中．好酒1升醉了3位客人，薄酒3升醉了1位客人，现在好酒和薄酒一共饮了19升，醉了33位客人，试问好酒、薄酒各有多少升？现在设好酒有 $x$ 升，薄酒有 $y$ 升，请你求出 $x$ 、 $y$ 的值分别是多少？

查看试题解析
20. 学史明理，学史增信，学史崇德，学史力行，在建党100周年之际，某校对全校学生进行了一次党史知识测试，成绩评定共分为A，B，C，D四个等级，随机抽取了部分学生的成绩进行调查，将获得的数据整理绘制成如下两幅不完整的统计图．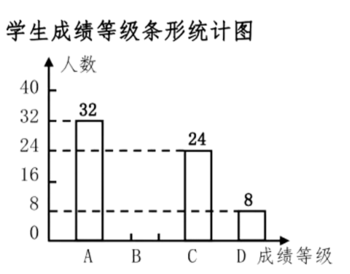
根据统计图提供的信息，解答下列问题：

(1)、在这次调查中一共抽取了名学生；

(2)、请根据以上信息直接在答题卡上补全条形统计图；

(3)、扇形统计图中，D等级对应的圆心角度数是度；

(4)、根据抽样调查的结果，请你估计该校2000学生中有多少名学生的成绩评定为C等级．

查看试题解析
21. 为实施乡村振兴战略，解决某山区老百姓出行难的问题，当地政府决定修建一条高速公路．其中一段长为144米的山体隧道贯穿工程由甲乙两个工程队负责施工．甲工程队独立工作2天后，乙工程队加入，两工程队又联合工作了1天，这3天共掘进23米．已知甲工程队每天比乙工程队多掘进1米，按此速度完成这项隧道贯穿工程，甲乙两个工程队还需联合工作多少天？

查看试题解析
22. 如图，已知点 $C$ 是线段 $A B$ 上一点，且 $A C = 2 C B$ ，点 $D$ 是 $A B$ 的中点，且 $A D = 6$ ，

(1)、求 $D C$ 的长；

(2)、若点 $F$ 是线段 $A B$ 上一点，且 $C F = \frac{1}{2} C D$ ，求 $A F$ 的长．

查看试题解析
23. 新定义：如图①，已知 $∠ A O B$ ，在 $∠ A O B$ 内部画射线OC，得到三个角，分别为 $∠ A O C$ 、 $∠ B O C$ 、 $∠ A O B$ ．若这三个角中有一个角是另外一个角的2倍，则称射线OC为 $∠ A O B$ 的“幸运线”．（本题中所研究的角都是大于0°而小于180°的角．）

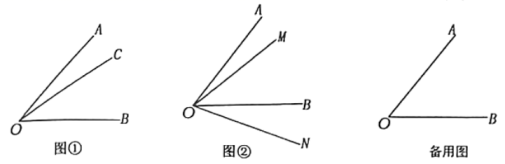(1)、（阅读理解）角的平分线这个角的“幸运线”；（填“是”或“不是”）

(2)、（初步应用）如图①， $∠ A O B = 48 °$ ，射线OC为 $∠ A O B$ 的“幸运线”，则 $∠ A O C$ 的度数为；（直接写出答案）

(3)、（解决问题）
如图②，已知 $∠ A O B = 50 °$ ，射线OM从OA出发，以每秒10°的速度绕O点顺时针旋转，同时，射线ON从OB出发，以每秒15°的速度绕O点顺时针旋转，设运动的时间为t秒 $(0 < t < 5)$ ．若OM、ON、OB三条射线中，一条射线恰好是以另外两条射线为边的角的“幸运线”，求运动的时间t的值．

(4)、（实际运用）
周末，小丽帮妈妈到附近的“中通快递”网点取包裹，出家门时小丽看了看时钟，恰好是下午3点整，取好包裹回到家时，小丽再看了看时钟，还没有到下午3点半，但此时分针与时针恰好重合．问小丽帮妈妈取包裹用了多少分钟？

查看试题解析