云南省文山壮族苗族自治州砚山县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 已知一个几何体的三视图如图所示，则该几何体是（）

A、棱柱 B、圆柱 C、圆锥 D、球

查看试题解析
2. 已知点 $P (2 ， - 3)$ 在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，则k的值是（）

A、6 B、 $- 6$ C、13 D、 $- 13$

查看试题解析
3. 如图， $A B$ 、 $C D$ 是⊙ $O$ 的两条弦，连接 $A D$ 、 $B C$ ．若∠ $B A D = 70 °$ ，则∠ $B C D$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
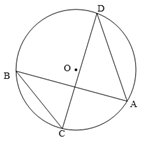4. 若抛物线 $y = - 7 (x + 4)^{2} - 1$ 平移得到 $y = - 7 x^{2}$ ，则必须（）

A、先向左平移4个单位，再向下平移1个单位 B、先向右平移4个单位，再向上平移1个单位 C、先向左平移1个单位，再向下平移4个单位 D、先向右平移1个单位，再向下平移4个单位

查看试题解析
5. 矩形ABCD的一条对角线长为6，边AB的长是方程 $x^{2} - 7 x + 10 = 0$ 的一个根，则矩形ABCD的面积为（）

A、 $2 \sqrt{6}$ B、12 C、 $8 \sqrt{2}$ D、 $8 \sqrt{2}$ 或 $5 \sqrt{11}$

查看试题解析
6. 如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系， $△ A B O$ 与 $△ A^{^{'}} B^{^{'}} O^{^{'}}$ 是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（）

A、 $(- 3 ， 2)$ B、 $(0 ， 1)$ C、 $(0 ， 0)$ D、 $(3 ， - 2)$

查看试题解析
7. 某公司去年的各项经营中，九月份的营业额为200万，十一月的营业额为950万元，如果平均每月营业额的增长率相同，设这个增长率为x，则可列方程得（）

A、 $200 x = 950$ B、 $200 (1 + x) = 950$ C、 $200 (1 + x)^{2} = 950$ D、 $200 + 200 (1 + x)^{2} = 950$

查看试题解析
8. 如图，两个反比例函数 $y_{1} = \frac{4}{x}$ 和 $y_{2} = \frac{2}{x}$ 在第一象限内的图象分别是 $C_{1}$ 和 $C_{2}$ ，设点P在 $C_{1}$ 上， $P A ⊥ x$ 轴于点A，交 $C_{2}$ 于点B，则 $△ P O B$ 的面积为（）

A、4 B、2 C、1 D、6

查看试题解析

二、填空题

9. 若关于x的一元二次方程 $x^{2} + x + m^{2} - 1 = 0$ 有一个根为0，则 $m =$ ．

查看试题解析
10. 一条弧所对的圆心角为 $120 °$ ，弧长等于 $6 π c m$ ，则这条弧的半径为．

查看试题解析
11. $△ A B C$ 和 $△ E B D$ 中， $\frac{A B}{E B} = \frac{B C}{B D} = \frac{A C}{E D} = \frac{5}{3}$ ， $△ E B D$ 的周长为 $10 c m$ ，则 $△ A B C$ 的周长为 $c m$ ．

查看试题解析
12. 如图，将宽为 $2 c m$ 的纸条沿BC折叠， $∠ C A B = 45 °$ ，则折叠后重叠部分的面积为．（根号保留）

查看试题解析
13. 已知一元二次方程x²－4x－3＝0的两根为m，n，则 $m^{2}$ －mn＋ $n^{2}$ =.

查看试题解析
14. 现规定一种新的运算： $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，当 $| \begin{array}{l} x & 3 \\ (x - 2) & x \end{array} | = 2 x$ 时，则x的值为．

查看试题解析

三、解答题

15. 计算：

(1)、 $2 x^{2} + 3 x - 9 = 0$ ；

(2)、 $\sqrt{18} - 6 s i n 45 ° + {(\frac{1}{2})}^{- 1} - (\sqrt{2} - 3)^{0}$ ．

查看试题解析
16. 如图，一次函数 $y_{1} = k x - 1$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于A，B两点，其中点A的坐标为 $(4 ， 2)$ ．

(1)、试确定k，m的值；

(2)、请写出当 $y_{1} > y_{2}$ 时，自变量x的取值范围．

查看试题解析

17. 某鞋店在一周内销售某款女鞋，尺码（单位：cm）数据收集如下：
24 23.5 21.5 23.5 24.5 23 22 23.5 23.5 23
22.5 23.5 23.5 22.5 24 24 22.5 25 23 23
23.5 23 22.5 23 23.5 23.5 23 24 22 22.5

绘制出不完整的频数分布表及频数分布直方图：

尺码/cm	划记	频数
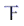
$21.5 ⩽ x < 22.5$		3
$22.5 ⩽ x < 23.5$	____	____
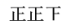
$23.5 ⩽ x < 24.5$		13
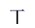
$24.5 ⩽ x < 25.5$		2

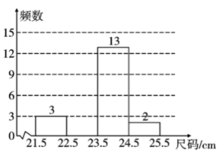(1)、请补全频数分布表和频数分布直方图；

(2)、若店主要进货，她最应该关注的是尺码的，上面数据的众数为；

(3)、若店主下周对该款女鞋进货200双，尺码在

23.5 ⩽ x < 25.5

范围的鞋应购进约多少双？

查看试题解析

18. 学好数学，就是为能更好解决生活中遇到的问题，如图所示，为了测量山的高度AC，在水平面E处测得山顶A的仰角为 $30 °$ ， $A C ⊥ E C$ ，自E沿着EC方向向前走 $100 m$ ，到达D处，又测得山顶A的仰角为 $45 °$ ，求山高．（结果保留根号）

查看试题解析
19. 将正面分别写着字母A，B，C的三张卡片（注：这三张卡片的形状、大小、质地、颜色等其它方面完全相同，若背面向上放在桌面上，这三张卡片看上去无任何差别）洗匀后，背面向上放在桌面上，从中先随机抽取一张卡片，记下卡片上的字母；放回卡片洗匀后，背面向上放在桌面上，再从卡片中随机抽取一张卡片，记下卡片上的字母．

(1)、用列表法或树状图法（树状图也称树形图）中的一种方法，写出所有可能出现的结果；

(2)、求取出的两张卡片上的字母相同的概率．

查看试题解析
20. 某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元，平均每天能售出32件，而当销售价每上涨1元，平均每天就少售出2件．

(1)、若公司每天的销售价为x元，则每天的销售量为多少？

(2)、该公司想要每天获得150元的销售利润，销售价应当为多少元？

(3)、如果物价部门规定这种零件的销售价不得高于每件28元，那么销售价定位多少元时，该公司每天获得的利润最大？最大利润是多少？

查看试题解析
21. 如图，已知AB是⊙O的直径， $B C ⊥ A B$ ，连接OC，弦 $A D ∥ O C$ ，直线CD交BA的延长线于点E．

(1)、求证：直线CD是⊙O的切线；

(2)、若 $D E = 2 B C$ ， $A D = 10$ ，求OC的长．

查看试题解析
22. 如图，四边形ABCD是菱形，点H为对角线AC的中点，点E在AB的延长线上， $C E ⊥ A B$ ，垂足为E，点F在AD的延长线上， $C F ⊥ A D$ ，垂足为 $F ， ∠ E C A = 60 °$ ．

(1)、求证：四边形CEHF是菱形；

(2)、已知四边形CEHF的周长为 $16 c m$ ，求菱形ABCD的面积．

查看试题解析
23. 抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于A、B两点，与y轴交于点C，点A的坐标为 $(- 1 ， 0)$ ，点C的坐标为 $(0 ， - 3)$ .点P为抛物线 $y = x^{2} + b x + c$ 上的一个动点.过点P作 $P D ⊥ x$ 轴于点D，交直线 $B C$ 于点E.

(1)、求b、c的值；

(2)、设点 $F$ 在抛物线 $y = x^{2} + b x + c$ 的对称轴上，当 $△ A C F$ 的周长最小时，直接写出点F的坐标；

(3)、在第一象限，是否存在点P，使点P到直线 $B C$ 的距离是点D到直线 $B C$ 的距离的5倍？若存在，求出点P所有的坐标；若不存在，请说明理由.

查看试题解析