上海市浦东新区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 某两地的距离为3000米,画在地图上的距离是15厘米,则地图上的距离与实际距离之比是( )A、1∶200 B、1∶2000 C、1∶20000 D、1∶2000002. 将抛物线y=﹣x2向右平移3个单位,再向下平移2个单位后所得新抛物线的顶点是( )A、(3,﹣2) B、(﹣3,﹣2) C、(3,2) D、(﹣3,2)3. 已知 , , 而且和的方向相反,那么下列结论中正确的是( )A、 B、 C、 D、4. 已知点P是线段AB的黄金分割点,且 , 则下列比例式能成立的是( )A、 B、 C、 D、5. 在离旗杆20米处的地方,用测角仪测得旗杆项的仰角为 , 如测角仪的高为1.5米,那么旗杆的高为( )米A、 B、 C、 D、6. 如图,在 中, , , 为 边上的一点,且 .若 的面积为 ,则 的面积为( )
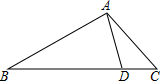 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 计算: .8. 在中, , , , 则 .9. 在一个边长为2的正方形中挖去一个小正方形,使小正方形四周剩下部分的宽度均为x,若剩下阴影部分的面积为y,那么y关于x的函数解析式是 .10. 抛物线y=ax2+ax+2(a≠0)的对称轴是直线 .11. 如果在平面直角坐标系xOy中,点P的坐标为(3,4),射线OP与X轴的正半轴所夹的角为α,那么α的余弦值等于 .12. 如图所示,在平行四边形ABCD中,F为BC中点,延长AD至E,使DE:AD=1:3,连结EF交DC于点G,则S△DEG:S△CFG等于.
 13. 已知二次函数(n为常数),若该函数图象与x轴只有一个公共点,则 .14. 如图,在Rt△ABC中,∠ACB=90°,点G是△ABC的重心,CG=2,sin∠ACG= ,则BC长为 .
13. 已知二次函数(n为常数),若该函数图象与x轴只有一个公共点,则 .14. 如图,在Rt△ABC中,∠ACB=90°,点G是△ABC的重心,CG=2,sin∠ACG= ,则BC长为 .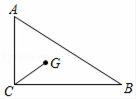 15. 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,设 , ,那么向量 关于 、 的分解式为 .
15. 如图,已知平行四边形ABCD的对角线AC与BD相交于点O,设 , ,那么向量 关于 、 的分解式为 . 16. 如图,在矩形ABCD中,AB=3,BC=4,点P为射线BC上的一个动点,过点P的直线PQ垂直于AP与直线CD相交于点Q , 当BP=5时,CQ= .
16. 如图,在矩形ABCD中,AB=3,BC=4,点P为射线BC上的一个动点,过点P的直线PQ垂直于AP与直线CD相交于点Q , 当BP=5时,CQ= . 17. 定义:直线与抛物线两个交点之间的距离称作抛物线关于直线的“割距”,如图,线段MN长就是抛物线关于直线的“割距”.已知直线与x轴交于点A,与y轴交于点B,点B恰好是抛物线的顶点,则此时抛物线关于直线y的割距是 .
17. 定义:直线与抛物线两个交点之间的距离称作抛物线关于直线的“割距”,如图,线段MN长就是抛物线关于直线的“割距”.已知直线与x轴交于点A,与y轴交于点B,点B恰好是抛物线的顶点,则此时抛物线关于直线y的割距是 . 18. 如图,a//b//c,直线a与直线b之间的距离为 , 直线c与直线b之间的距离为 , 等边的三个顶点分别在直线a、直线b、直线c上,则等边三角形的边长是 .
18. 如图,a//b//c,直线a与直线b之间的距离为 , 直线c与直线b之间的距离为 , 等边的三个顶点分别在直线a、直线b、直线c上,则等边三角形的边长是 .
三、解答题
-
19. 求值:(结果保留根号).20. 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,且DE= BC.
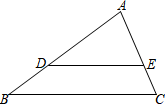 (1)、如果AC=6,求AE的长;(2)、设 , ,求向量 (用向量 、 表示).21. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)的山坡AB上发现棵古树CD,测得古树底端C到山脚点A的距离m,在距山脚点A处水平距离6m的点E处测得古树顶端D的仰角(古树CD与山坡AB的剖面、点E在同一平面上,古树CD所在直线与直线AE垂直),则古树CD的高度约为多少米?(结果精确到整数)(数据 , , )
(1)、如果AC=6,求AE的长;(2)、设 , ,求向量 (用向量 、 表示).21. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)的山坡AB上发现棵古树CD,测得古树底端C到山脚点A的距离m,在距山脚点A处水平距离6m的点E处测得古树顶端D的仰角(古树CD与山坡AB的剖面、点E在同一平面上,古树CD所在直线与直线AE垂直),则古树CD的高度约为多少米?(结果精确到整数)(数据 , , )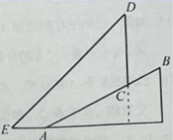 22. 如图,在Rt△ABC中,∠ACB=90°,AC=6,cosA= . D是AB边的中点,过点D作直线CD的垂线,与边BC相交于点E.
22. 如图,在Rt△ABC中,∠ACB=90°,AC=6,cosA= . D是AB边的中点,过点D作直线CD的垂线,与边BC相交于点E. (1)、求线段CE的长;(2)、求sin∠BDE的值.23. 如图,在和中, , , AC与DE相交于点F,联结CE,点D在边BC上.
(1)、求线段CE的长;(2)、求sin∠BDE的值.23. 如图,在和中, , , AC与DE相交于点F,联结CE,点D在边BC上. (1)、求证:∽;(2)、若 , 求的值.
(1)、求证:∽;(2)、若 , 求的值.


