上海市奉贤区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系xOy中，下列函数的图象过点（-1，1）的是（）

A、 $y = x - 1$ B、 $y = - x + 1$ C、 $y = \frac{1}{x}$ D、 $y = x^{2}$

查看试题解析
2. 从图形运动的角度研究抛物线，有利于我们认识新的拋物线的特征. 如果将拋物线 $y = x^{2} + 2$ 绕着原点旋转180°，那么关于旋转后所得新抛物线与原抛物线之间的关系，下列法正确的是（）

A、它们的开口方向相同 B、它们的对称轴相同 C、它们的变化情况相同 D、它们的顶点坐标相同

查看试题解析
3. 如果直线 $y = 2 x$ 与 x 轴正半轴的夹角为锐角 $α$ ，那么下列各式正确的是（）

A、 $s i n α = \frac{1}{2}$ B、 $c o s α = \frac{1}{2}$ C、 $t a n α = \frac{1}{2}$ D、 $c o t α = \frac{1}{2}$

查看试题解析
4. 如图，已知 D 是 $△ A B C$ 边 $A B$ 上的一点，如果 $∠ B C D = ∠ A$ ，那么下列结论中正确的是（）

A、 $A C^{2} = A D \cdot A B$ B、 $B C^{2} = B D \cdot A B$ C、 $C D^{2} = A D \cdot B D$ D、 $A D^{2} = B D \cdot C D$

查看试题解析
5. 已知线段 $A B$ ．按以下步骤作图：
⑴作以A为端点的射线 $A P$ （不与线段 $A B$ 所在直线重合）；
⑵在射线 $A P$ 上顺次截取 $A C = C D = D E$ ；
⑶联结 $B E$ ，过点 D 作 $D F / / B E$ ，交线段 $A B$ 于点 F．
根据上述作图过程，下列结论中正确的是（）

A、 $A F ： A B = 1 ： 2$ B、 $A F ： A B = 1 ： 3$ C、 $A F ： A B = 2 ： 3$ D、 $A F ： A B = 2 ： 1$ .

查看试题解析
6. 在 $△ A B C$ 中， $A B = 2 \sqrt{3} ， ∠ B A C = 3 0^{∘}$ . 下列线段 $B C$ 的长度不能使 $△ A B C$ 的形状和大小都确定的是（）

A、2 B、4 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

7. 如果 $\frac{x}{2} = \frac{y}{3} = \frac{z}{5} \neq 0$ ，那么 $\frac{y - x}{z} =$ ．

查看试题解析
8. 函数 $y = \frac{x}{x + 1}$ 的定义域是．

查看试题解析
9. 计算：2（ $\vec{a}$ ﹣2 $\vec{b}$ ）+3（ $\vec{a}$ + $\vec{b}$ ）＝．

查看试题解析
10. 如果函数y＝kx（k≠0）的图象经过第二、四象限，那么y的值随x的值增大而．（填“增大”或“减小”）

查看试题解析
11. 如果抛物线 $y = {(x - 2)}^{2} + k$ 不经过第三象限，那么k的值可以是．（只需写一个）

查看试题解析
12. 用描点法画二次函数的图象需要经过列表、描点、连线三个步骤. 以下是小明画二次函数 $y = a x^{2} + b x + c$ 图像时所列的表格：
$x$
$\dots$
$- 4$
$- 3$
$- 2$
0
2
$\dots$
$y$
$\dots$
3
0
$- 1$
3
15
$\dots$
根据表格可以知道该二次函数图象的顶点坐标是．

查看试题解析
13. 如图，已知 $A D ∥ B E ∥ C F$ ，它们依次交直线 $l_{1} 、 l_{2}$ 于点 $A 、 B 、 C$ 和点 $D 、 E 、 F$ . 如果 $5 A B = 2 A C ， D E = 6$ ，那么线段 $E F$ 的长是．

查看试题解析
14. 已知在△ABC中，∠C=90°，sinA= $\frac{3}{4}$ ，BC=6，则AB的长是．

查看试题解析
15. 联结三角形各边中点，所得的三角形的周长与原三角形周长的比是.

查看试题解析
16. 如图，已知菱形ABCD，E、F分别为 △ABD和△CBD的重心，如果边AB=5，对角线BD=6，那么EF的长为．

查看试题解析
17. 《九章算术》是我国古代的数学名著，书中有这样一个问题：“今有邑方不知大小，各中开门，出北门一百步立一表，出西门二百二十五步适可见之，问邑方几何? ” 它的意思是：如图 $， M$ 、N分别是正方形 $A B C D$ 的边 $A D ， A B$ 的中点， $M E ⊥ A D ， N F ⊥ A B ， E F$ 过点 A，且 $M E = 100$ 步， $N F = 225$ 步，那么该正方形城邑边长 $A D$ 约为步．

查看试题解析
18. 如图，在 Rt $△ A B C$ 中， $∠ C = 9 0^{∘} ， s i n B = \frac{3}{5} ． D$ 是边 $B C$ 的中点，点 E 在边 $A B$ 上，将 $△ B D E$ 沿直线 $D E$ 翻折，使得点 B 落在同一平面内的点 F 处. 如果线段 $F D$ 交边 $A B$ 于点 G，当 $F D ⊥ A B$ 时， $A E ： B E$ 的值为．

查看试题解析

三、解答题

19. 计算： $\frac{2 s i n^{2} 6 0^{∘} - \frac{1}{2} c o t 4 5^{∘}}{t a n^{2} 6 0^{∘} + 4 s i n 4 5^{∘}} ．$

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，矩形 $A B C D$ 的顶点 $A (4 ， 0)$ 和 B 在 x 轴的正半轴上，反比例函数 $y = \frac{k}{x}$ 在第一象限内的图像经过点D，交 $B C$ 于点 $E . C E = 2 B E ， t a n ∠ A O D = \frac{3}{4}$ ．

(1)、求反比例函数的解析式；

(2)、连接 $O C$ ，求 $∠ B O C$ 的正切值．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A C = 5 ， c o t A = 2 ， c o t B = 3$ ， D是 $A B$ 边上的一点， $∠ B D C = 45 °$ ．

(1)、求线段 $B D$ 的长；

(2)、如果设 $\vec{C A} = a ， \vec{C B} = b$ ，那么 $\vec{A B} = Δ$ ， $\vec{A D} = Δ ， \vec{C D} = Δ ．$ （含 $a 、 b$ 的式子表示）．

查看试题解析
22. 如图是位于奉贤南桥镇解放东路 866 号的 “奉贤电视发射塔”，它建于 1996 年，在长达二十几年的时间里它一直是奉贤区最高建筑物，该记录一直保持到 2017年，历了25 年风雨的电视塔铎刻了一代奉贤人的记忆．
某数学活动小组在学习了 “解直角三角形的应用” 后，开展了测量“奉贤电视发射塔的高度”的实践活动．
测量方案：如图，在电视塔附近的高楼楼顶 C 处测量塔顶 A 处的仰角和塔底 B 处的俯角．
数据收集：这幢高楼共 12 层，每层高约 $2.8$ 米，在高楼楼项 C 处测得塔顶 A 处的仰角为 $5 8^{∘}$ ，塔底 B 处的俯角为 $2 2^{∘}$ .
问题解决：求奉贤电视发射塔 $A B$ 的高度（结果精确到 1 米）．
参考数据： $s i n 2 2^{∘} \approx 0.37 ， c o s 2 2^{∘} \approx 0.93$ ， $t a n 2 2^{∘} \approx 0.40 ， s i n 5 8^{∘} \approx 0.85$ ， $c o s 5 8^{∘} \approx 0.53 ， t a n 5 8^{∘} \approx 1.60$ ．
根据上述测量方案及数据，请你完成求解过程．

查看试题解析
23. 根据相似形的定义可以知道，如果一个四边形的四个角与另一个四边形的四个角对应相等，且它们各有的四边对应成比例，那么这两个四边形叫做相似四边形. 对应相等的角的顶点叫做这两个相似四边形的对应顶点，以对应顶点为端点的边是这两个相似四边形的对应边，对应边的比叫做这两个相似多边形的相似比．（我们研究的四边形都是指凸四边形）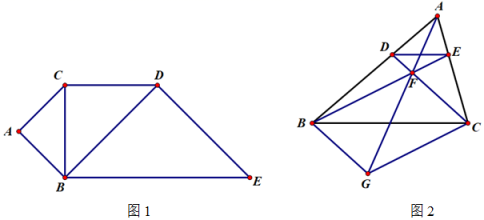

(1)、某学习小组在探究相似四边形的判定时，得到如下两个命题，请判断它们是真命题还是假命题（直接在横线上填写“真”或“假”）
①梯形的中位线将原梯形分成的两个小的梯形相似；
②有一个内角对应相等的两个菱形相似；

(2)、已知：如图1， $△ A B C$ 是以 $B C$ 为斜边的等腰直角三角形，以 $B C$ 为直角边作等腰直角三角形 $B C D$ ，再以 $B D$ 为直角边作等腰直角三角形 $B D E$ ．
求证：四边形 $A B D C$ 与四边形 $C B E D$ 相似．

(3)、已知：如图2，在 $△ A B C$ 中，点 $D 、 E$ 分别在边 $A B 、 A C$ 上， $B E 、 C D$ 相交于点F，点 $G$ 在 $A F$ 的延长线上，联结 $B G 、 C G .$ 如果四边形 $A D F E$ 与四边形 $A B G C$ 相似，且点 $A 、 D 、 F 、 E$ 分别对应 $A 、 B 、 G 、 C$ ．
求证： $A F · B F = A G \cdot E F$ ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x + 3$ 与x轴交于点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，与y轴交于点C，顶点为D．

(1)、求该抛物线的表达式的顶点D的坐标；

(2)、将抛物线沿y轴上下平移，平移后所得新拋物线顶点为M，点C的对应点为E．
①如果点M落在线段 $B C$ 上，求 $∠ D B E$ 的度数；
②设直线 $M E$ 与x轴正半轴交于点P，与线段 $B C$ 交于点Q，当 $P E = 2 P Q$ 时，求平移后新抛物线的表达式．

查看试题解析
25. 如图1，已知锐角△ABC的高AD、BE相交于点F，延长AD至G，使DG=FD，连接BG，CG．

(1)、求证： $B D \cdot A C = A D \cdot B G$ ；

(2)、如果 $B C = 10$ ，设 $t a n ∠ A B C = m$ ．
①如图2，当∠ABG=90°时，用含m的代数式表示△BFG的面积；
②当AB=8，且四边形BGCE是梯形时，求m的值．

查看试题解析

$x$	$\dots$	$- 4$	$- 3$	$- 2$	0	2	$\dots$
$y$	$\dots$	3	0	$- 1$	3	15	$\dots$