山西省晋中市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断2. 刘徽是中国历史上最杰出的数学家之一,他的一部专著是中国最早的测量数学专著,使中国的测量学达到了世界的巅峰.这部著作是( )
 A、《周髀算经》 B、《九章算术》 C、《孙子算经》 D、《海岛算经》3. 在我们日常生活中存在很多较小的或眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )
A、《周髀算经》 B、《九章算术》 C、《孙子算经》 D、《海岛算经》3. 在我们日常生活中存在很多较小的或眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( ) A、平移变换 B、旋转变换 C、轴对称变换 D、相似变换4. 已知点 , 都是反比例函数图象上的点,则与的大小关系为( )A、 B、 C、 D、无法确定5. 如图,该几何体的左视图是( )
A、平移变换 B、旋转变换 C、轴对称变换 D、相似变换4. 已知点 , 都是反比例函数图象上的点,则与的大小关系为( )A、 B、 C、 D、无法确定5. 如图,该几何体的左视图是( )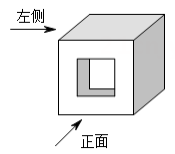 A、
A、 B、
B、 C、
C、 D、
D、 6. 绿丝带是颜色丝带的一种,被用来象征许多事物,例如环境保护、大麻和解放农业等,同时绿丝带也代表健康,使人对健康的人生与生命的活力充满无限希望.某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图所示,丝带重叠部分形成的图形是( )
6. 绿丝带是颜色丝带的一种,被用来象征许多事物,例如环境保护、大麻和解放农业等,同时绿丝带也代表健康,使人对健康的人生与生命的活力充满无限希望.某班同学在“做环保护航者”的主题班会课上制作象征“健康快乐”的绿丝带(丝带的对边平行且宽度相同),如图所示,丝带重叠部分形成的图形是( ) A、矩形 B、菱形 C、正方形 D、等腰梯形7. 如图是一个闭合电路,其电源的电压为定值,电流I(A)是电阻R()的反比例函数.当时, . 若电阻R增大 , 则电源I为( )
A、矩形 B、菱形 C、正方形 D、等腰梯形7. 如图是一个闭合电路,其电源的电压为定值,电流I(A)是电阻R()的反比例函数.当时, . 若电阻R增大 , 则电源I为( ) A、3A B、4A C、7A D、12A8. 为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为( )A、 B、 C、 D、9. 快递作为现代服务业的重要组成部分,在国家经济社会发展和改善民生方面发挥了越来越重要的作用,其中顺丰、韵达、圆通、申通的业务量增速较快,成为我国快递的“四大龙头”企业,随着市场竞争逐渐激烈,低价竞争成为主流,快递的平均单价从2019年的12元/件连续降价至2021年的9.72元/件,设快递单价每年降价的百分率均为 , 则所列方程为( )
A、3A B、4A C、7A D、12A8. 为了深化落实“双减”工作,促进中小学生健康成长,教育部门加大了实地督查的力度,对我校学生的作业、睡眠、手机、读物、体质“五项管理”要求的落实情况进行抽样调查,计划从“五项管理”中随机抽取两项进行问卷调查,则抽到“作业”和“手机”的概率为( )A、 B、 C、 D、9. 快递作为现代服务业的重要组成部分,在国家经济社会发展和改善民生方面发挥了越来越重要的作用,其中顺丰、韵达、圆通、申通的业务量增速较快,成为我国快递的“四大龙头”企业,随着市场竞争逐渐激烈,低价竞争成为主流,快递的平均单价从2019年的12元/件连续降价至2021年的9.72元/件,设快递单价每年降价的百分率均为 , 则所列方程为( ) A、 B、 C、 D、10. 如图,在中,点E是边上一点,且 , 与交于点F,则与的面积之比是( )
A、 B、 C、 D、10. 如图,在中,点E是边上一点,且 , 与交于点F,则与的面积之比是( ) A、2:3 B、4:9 C、4:15 D、9:15
A、2:3 B、4:9 C、4:15 D、9:15二、填空题
-
11. 若 ,则 =12. 皮影戏是一种以兽皮或纸板做成的人物剪影,在灯光照射下用隔亮布进行表演的民间戏剧.表演者在幕后操纵剪影、演唱,或配以音乐,具有浓厚的乡土气息.“皮影戏”中的皮影是(填写“平行投影”或“中心投影”)
 13. 第24届世界冬季奥林匹克运动会,于2022年2月4日在中国北京市和河北省张家口市联合举行,其会徽为“冬梦”,这是中国历史上首次举办冬季奥运会.如图,是一幅印有北京冬奥会会徽且长为3m,宽为2m的长方形宣传画,为测量宣传画上会徽图案的面积,现将宣传画平铺,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在会徽图案上的频率稳定在0.15左右,由此可估计宣传画上北京冬奥会会徽图案的面积约为 .
13. 第24届世界冬季奥林匹克运动会,于2022年2月4日在中国北京市和河北省张家口市联合举行,其会徽为“冬梦”,这是中国历史上首次举办冬季奥运会.如图,是一幅印有北京冬奥会会徽且长为3m,宽为2m的长方形宣传画,为测量宣传画上会徽图案的面积,现将宣传画平铺,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在会徽图案上的频率稳定在0.15左右,由此可估计宣传画上北京冬奥会会徽图案的面积约为 . 14. 榆社文峰塔位于晋中市榆社县城东南的巽山之上,建于清代康熙年间,文峰塔不仅构思奇特,工艺精巧,而且选址巧妙,寓意深远.老师希望同学们利用所学过的知识测量文峰塔的高度,为此数学兴趣小组的同学们设计了如图所示的测量示意图,并测出竹竿长2米,在太阳光下,它的影长为1.5米,同一时刻,测得文峰塔的影长约为28.5米,请根据测量数据计算出文峰塔的高度约为米.
14. 榆社文峰塔位于晋中市榆社县城东南的巽山之上,建于清代康熙年间,文峰塔不仅构思奇特,工艺精巧,而且选址巧妙,寓意深远.老师希望同学们利用所学过的知识测量文峰塔的高度,为此数学兴趣小组的同学们设计了如图所示的测量示意图,并测出竹竿长2米,在太阳光下,它的影长为1.5米,同一时刻,测得文峰塔的影长约为28.5米,请根据测量数据计算出文峰塔的高度约为米.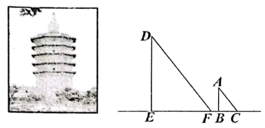 15. 如图,四边形是正方形,在y轴的正半轴上,在x轴的负半轴上,反比例函数在第二象限的图象与 , 分别交于点E,F.若 , 则线段的长为 .
15. 如图,四边形是正方形,在y轴的正半轴上,在x轴的负半轴上,反比例函数在第二象限的图象与 , 分别交于点E,F.若 , 则线段的长为 .
三、解答题
-
16.(1)、解方程: .(2)、阅读下列材料,并完成相应任务.
三国时期的数学家赵爽在其所落的《勾股圆方图注》中记载了一元二次方程的几何解法,以 为例,说明如下:
将方程 变形为 , 然后画四个长为 , 宽为x的矩形,按如图所示的方式拼成一个“空心”大正方形.图中大正方形的面积可表示为 , 还可表示为四个矩形与一个边长为2的小正方形面积之和,即: ,
可得新方程: ,
∵x表示边长,
∴ .
∴ .

任务一:①这种构造图形解一元二次方程的方法体现的数学思想是 ;
A.分类讨论思想 B.数形结合思想 C.演绎思想 D.公理化思想
②用配方法解方程: .
任务二:比较上述两种解一元二次方程的方法,请反思利用构造图形的方法求解一元二次方程的不足之处是 . (写出一条即可)
17. 如图所示,小华在学习《图形的位似》时,利用几何画板软件,在平面直角坐标系中画出了的位似图形 . (1)、在图中标出与的位似中心点的位置,并写出点的坐标;(2)、若以点为位似中心,请你帮小华在图中给定的网格内画出的位似图形 , 且与的位似比为2:1.18. 电影《长津湖》以抗美援朝战争第二次战役中的长津湖战役为背景,讲述71年前,中国人民志愿军赴朝作战,在极寒严酷环境下,东线作战部队凭着钢铁意志和英勇无畏的战斗精神一路追击,奋勇杀敌的真实历史.为纪念历史,缅怀先烈,我校团委将电影中的四位历史英雄人物头像制成编号为A、B、C、D的四张卡片(除编号和头像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在影片中波澜壮阔、可歌可泣的历史事迹.规则如下:先将四张卡片背面朝上,洗匀放好,小强从中随机抽取一张,然后放回并洗匀,小叶再从中随机抽取一张.请用列表或画树状图的方法求小强和小叶抽到的两张卡片恰好是同一英雄人物的概率.
(1)、在图中标出与的位似中心点的位置,并写出点的坐标;(2)、若以点为位似中心,请你帮小华在图中给定的网格内画出的位似图形 , 且与的位似比为2:1.18. 电影《长津湖》以抗美援朝战争第二次战役中的长津湖战役为背景,讲述71年前,中国人民志愿军赴朝作战,在极寒严酷环境下,东线作战部队凭着钢铁意志和英勇无畏的战斗精神一路追击,奋勇杀敌的真实历史.为纪念历史,缅怀先烈,我校团委将电影中的四位历史英雄人物头像制成编号为A、B、C、D的四张卡片(除编号和头像外其余完全相同),活动时学生根据所抽取的卡片来讲述他们在影片中波澜壮阔、可歌可泣的历史事迹.规则如下:先将四张卡片背面朝上,洗匀放好,小强从中随机抽取一张,然后放回并洗匀,小叶再从中随机抽取一张.请用列表或画树状图的方法求小强和小叶抽到的两张卡片恰好是同一英雄人物的概率. 19. 如图,在中, , 是的中线,点E是的中点,过点C作CF∥AB交的延长线于点F,连接 . 请判断四边形的形状,并加以证明.
19. 如图,在中, , 是的中线,点E是的中点,过点C作CF∥AB交的延长线于点F,连接 . 请判断四边形的形状,并加以证明. 20. 如图,一次函数的图象与反比例函数的图象交于 , B两点,与y轴交于点C.
20. 如图,一次函数的图象与反比例函数的图象交于 , B两点,与y轴交于点C. (1)、求反比例函数的表达式;(2)、求出点B的坐标,并直接写出的面积;(3)、根据图象,请直接写出不等式的解集.21. 2021年12月9日,在神舟十三号载人飞船上,翟志刚、王亚平、叶光富三位航天员为广大青少年开讲“天宫课堂”第一课,这是中国空间站首次太空授课活动.在此期间,我校“对话太空”兴趣小组举行了航天科普知识有奖竞答活动,并购买“神舟载人飞船”模型作为奖品,学校在商店里了解到:如果一次性购买数量不超过10个,每个模型的单价为40元;如果一次性购买数量超过10个,每多购买一个,每个模型的单价均降低0.5元,但每个模型最低单价不低于30元,若学校为购买“神舟载人飞船”模型一次性付给商店900元,请求出学校购买“神舟载人飞船”模型的数量.
(1)、求反比例函数的表达式;(2)、求出点B的坐标,并直接写出的面积;(3)、根据图象,请直接写出不等式的解集.21. 2021年12月9日,在神舟十三号载人飞船上,翟志刚、王亚平、叶光富三位航天员为广大青少年开讲“天宫课堂”第一课,这是中国空间站首次太空授课活动.在此期间,我校“对话太空”兴趣小组举行了航天科普知识有奖竞答活动,并购买“神舟载人飞船”模型作为奖品,学校在商店里了解到:如果一次性购买数量不超过10个,每个模型的单价为40元;如果一次性购买数量超过10个,每多购买一个,每个模型的单价均降低0.5元,但每个模型最低单价不低于30元,若学校为购买“神舟载人飞船”模型一次性付给商店900元,请求出学校购买“神舟载人飞船”模型的数量. 22. 综合与实践
22. 综合与实践问题情境:
数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽 .
 (1)、动手实践:
(1)、动手实践:如图1,腾飞小组将矩形纸片折叠,点A落在边上的点处,折痕为 , 连接 , 然后将纸片展平,得到四边形 . 试判断四边形的形状,并加以证明.
(2)、如图2,永攀小组在矩形纸片的边上取一点F,连接 , 使 , 将沿线段折叠,使点C正好落在边上的点G处.连接 , , 将纸片展平,①求的面积;
②连接 , 线段与线段交于点M,则 ▲ .
(3)、深度探究:如图3,探究小组将图1的四边形剪下,在边上取一点N,使 , 将沿线段折叠得到 , 连接 , 探究并直接写出的长度.
23. 综合与探究如图,矩形的顶点O与坐标原点重合,边 , 分别落在轴和轴上,顶点B的坐标(8,4),点D是边上一动点,过点D作反比例函数的图象与矩形的边交于点E.
 (1)、如图1,连接 , , 若 .
(1)、如图1,连接 , , 若 .①填空:点D的坐标为 ▲ , 点E的坐标为 ▲ ;
②请判断线段与的位置关系,并说明理由.
(2)、如图2,连接 , , 若线段平分 .①求k的值;
②若动点M在y轴上运动,当线段与的差最大时,请直接写出点M的坐标.