山西省大同市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、

B、
B、
C、
C、
D、
D、
2. 下列事件中,属于必然事件的是( )A、任意购买一张电影票,座位号是奇数 B、抛一枚硬币,正面朝上 C、五个人分成四组,这四组中有一组必有2人 D、打开电视,正在播放动画片3. 抛物线的对称轴为直线( )A、 B、 C、 D、4. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、无实数根5. 古希腊数学家、天文学家泰勒斯曾在金字塔影子的顶部立一根木杆,借助太阳光线利用数学原理,来测量金字塔的高度.如图,在某一时刻,测得木杆EF的长为2m,它的影长FD为3m,同时测得OA为201 m,求金字塔的高度BO.在解决这个问题的过程中,主要运用的数学知识是( )
2. 下列事件中,属于必然事件的是( )A、任意购买一张电影票,座位号是奇数 B、抛一枚硬币,正面朝上 C、五个人分成四组,这四组中有一组必有2人 D、打开电视,正在播放动画片3. 抛物线的对称轴为直线( )A、 B、 C、 D、4. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、无实数根5. 古希腊数学家、天文学家泰勒斯曾在金字塔影子的顶部立一根木杆,借助太阳光线利用数学原理,来测量金字塔的高度.如图,在某一时刻,测得木杆EF的长为2m,它的影长FD为3m,同时测得OA为201 m,求金字塔的高度BO.在解决这个问题的过程中,主要运用的数学知识是( ) A、图形的轴对称 B、图形的平移 C、图形的旋转 D、图形的相似6. 如图,已知太原南站某自动扶梯AB的倾斜角为31°,自动扶梯AB的长为15 m,则大厅两层之间的高度BC为( )
A、图形的轴对称 B、图形的平移 C、图形的旋转 D、图形的相似6. 如图,已知太原南站某自动扶梯AB的倾斜角为31°,自动扶梯AB的长为15 m,则大厅两层之间的高度BC为( ) A、 B、 C、 D、7. 已知点在反比例函数的图象上,则下列说法正确的是( )A、图象位于第一、三象限 B、点(2,6)在该函数图象上 C、当时,y随x的增大而增大 D、当时,8.
A、 B、 C、 D、7. 已知点在反比例函数的图象上,则下列说法正确的是( )A、图象位于第一、三象限 B、点(2,6)在该函数图象上 C、当时,y随x的增大而增大 D、当时,8.如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( )
 A、15 B、10 C、 D、59. 如图,AB是的直径,的弦DC的延长线与AB的延长线相交于点P,于点E, , , 则阴影部分的面积为( )
A、15 B、10 C、 D、59. 如图,AB是的直径,的弦DC的延长线与AB的延长线相交于点P,于点E, , , 则阴影部分的面积为( ) A、 B、 C、 D、10. 已知二次函数的图象如图所示,则下列结论正确的是( )
A、 B、 C、 D、10. 已知二次函数的图象如图所示,则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在中, , , 则的度数是 .12. 如图,某小区车库出入口的栏杆短臂 长1m,长臂 长8m,当短臂外端 下降0.5m时,长臂外端 升高.
 13. 合作小组的4位同学在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则B坐在2号座位的概率是 .
13. 合作小组的4位同学在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则B坐在2号座位的概率是 . 14. 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
14. 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .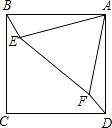 15. 如图,点O是的AB边上一点, , 以OB长为半径作 , 与AC相切于点D.若 , , 则的半径长为 .
15. 如图,点O是的AB边上一点, , 以OB长为半径作 , 与AC相切于点D.若 , , 则的半径长为 .
三、解答题
-
16.(1)、计算:;(2)、解方程: .17. 如图,一次函数的图象与反比例函数的图象相交于A(1,3),B(3,n)两点,与两坐标轴分别相交于点P,Q,过点B作于点C,连接OA.
 (1)、求一次函数和反比例函数的解析式;(2)、求四边形ABCO的面积.18. 如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部BC垂直于墙面CD,且当导风板所在的直线AE与竖直直线AB的夹角α为42°时,空调风刚好吹到床的外边沿E处,于点D,于点F.若 , , 床铺 , 求空调机的底部位置距离床的高度CD.(结果精确到0.1m,参考数据: , , )
(1)、求一次函数和反比例函数的解析式;(2)、求四边形ABCO的面积.18. 如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部BC垂直于墙面CD,且当导风板所在的直线AE与竖直直线AB的夹角α为42°时,空调风刚好吹到床的外边沿E处,于点D,于点F.若 , , 床铺 , 求空调机的底部位置距离床的高度CD.(结果精确到0.1m,参考数据: , , ) 19. 小军准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形,设其中一个正方形的边长为x cm,这两个正方形的面积之和为 . 请解答下列问题:(1)、另一个正方形的边长为cm(用含x的代数式表示);(2)、要使这两个正方形的面积之和等于 , 小军应怎么剪?(3)、小华对小军说:“这两个正方形的面积之和的最小值为 . ”他的说法符合题意吗?请说明理由.20. 太原是国家历史文化名城,有很多旅游的好去处,周末哥哥计划带弟弟出去玩,放假前他收集了太原动物园、晋祠公园、森林公园、汾河湿地公园四个景点的旅游宣传卡片,这些卡片的大小、形状及背面完全相同,分别用D,J,S,F表示,如图所示,请用列表或画树状图的方法,求下列事件发生的概率.
19. 小军准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形,设其中一个正方形的边长为x cm,这两个正方形的面积之和为 . 请解答下列问题:(1)、另一个正方形的边长为cm(用含x的代数式表示);(2)、要使这两个正方形的面积之和等于 , 小军应怎么剪?(3)、小华对小军说:“这两个正方形的面积之和的最小值为 . ”他的说法符合题意吗?请说明理由.20. 太原是国家历史文化名城,有很多旅游的好去处,周末哥哥计划带弟弟出去玩,放假前他收集了太原动物园、晋祠公园、森林公园、汾河湿地公园四个景点的旅游宣传卡片,这些卡片的大小、形状及背面完全相同,分别用D,J,S,F表示,如图所示,请用列表或画树状图的方法,求下列事件发生的概率. (1)、把这四张卡片背面朝上洗匀后,弟弟从中随机抽取一张,作好记录后,将卡片放回洗匀,哥哥再抽取一张,求两人抽到同一景点的概率;(2)、把这四张卡片背面朝上洗匀后,弟弟和哥哥从中各随机抽取一张(不放回),求两人抽到动物园和森林公园的概率.21. 请阅读下面材料,并完成相应的任务;
(1)、把这四张卡片背面朝上洗匀后,弟弟从中随机抽取一张,作好记录后,将卡片放回洗匀,哥哥再抽取一张,求两人抽到同一景点的概率;(2)、把这四张卡片背面朝上洗匀后,弟弟和哥哥从中各随机抽取一张(不放回),求两人抽到动物园和森林公园的概率.21. 请阅读下面材料,并完成相应的任务;阿基米德折弦定理
阿基米德(Arehimedes,公元前287—公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.

阿拉伯Al-Biruni(973年—1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》,第一题就是阿基米德的折弦定理.
阿基米德折弦定理:如图1,AB和BC是的两条弦(即折线ABC是圆的一条折弦), , M是的中点,则从点M向BC所作垂线的垂足D是折弦ABC的中点,即 .
这个定理有很多证明方法,下面是运用“垂线法”证明的部分证明过程.

证明:如图2,过点M作射线AB,垂足为点H,连接MA,MB,MC.
∵M是的中点,
∴ .
…
任务:
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、如图3,已知等边三角形ABC内接于 , D为上一点, , 于点E, , 连接AD,则的周长是 . 22. 综合与实践
22. 综合与实践问题情境:
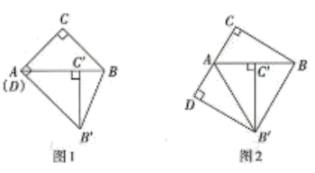
数学活动课上,同学们将绕点A顺时针旋转得到 , 点落在边AB上,连接 , 过点作于点D.
特例分析:
(1)、如图1,若点D与点A重合,请判断线段AC与BC之间的数量关系,并说明理由;探索发现:
(2)、如图2,若点D在线段CA的延长线上.且 , 请判断线段AD与之间的数最关系,并说明理由.23. 综合与探究如图,已知抛物线与x轴相交于点A,B(点B在点A的右侧),与y轴相交于点C,其顶点为点D,连接AC,BC.
 (1)、求点A,B,D的坐标;(2)、设抛物线的对称轴DE交线段BC于点E,P为第四象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F.若四边形DEFP为平行四边形,求点P的坐标;(3)、设点M是线段BC上的一个动点,过点M作 , 交AC于点N.点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t()秒,直接写出当t为何值时,为等腰直角三角形.
(1)、求点A,B,D的坐标;(2)、设抛物线的对称轴DE交线段BC于点E,P为第四象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F.若四边形DEFP为平行四边形,求点P的坐标;(3)、设点M是线段BC上的一个动点,过点M作 , 交AC于点N.点Q从点B出发,以每秒1个单位长度的速度沿线段BA向点A运动,运动时间为t()秒,直接写出当t为何值时,为等腰直角三角形.