内蒙古通辽市科尔沁左翼中旗2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 已知 $⊙ O$ 的半径为5cm，点P到圆心O的距离为4cm，则点P和圆的位置关系（）

A、点在圆内 B、点在圆外 C、点在圆上 D、无法判断

查看试题解析
3. 二次函数的图象 $y = {(x + 3)}^{2} - 2$ 的顶点坐标是（）

A、（3，2） B、（﹣3，2） C、（﹣3，﹣2） D、（3，﹣2）

查看试题解析
4. 一元二次方程 $x^{2} - 2 x - 1 = 0$ 的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
5. 某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（）．

A、20% B、40% C、18% D、36%

查看试题解析
6. 如图，在⊙O中，点A是 $\overset{⌢}{C B}$ 的中点，∠AOB＝40°，则∠ADC的度数是（）

A、15° B、20° C、25° D、40°

查看试题解析
7. 把函数 $y = - \frac{1}{2} x^{2}$ 的图象，经过怎样的平移变换以后，可以得到函数 $y = - \frac{1}{2} {(x - 1)}^{2} + 1$ 的图象（）

A、向左平移 $1$ 个单位，再向下平移 $1$ 个单位 B、向左平移 $1$ 个单位，再向上平移 $1$ 个单位 C、向右平移 $1$ 个单位，再向上平移 $1$ 个单位 D、向右平移 $1$ 个单位，再向下平移 $1$ 个单位

查看试题解析
8. 某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用长为40米的篱笆围成，已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边的长为x米，围成的苗圃面积为y，则y关于x的函数关系式为（）

A、y＝x（40－x） B、y＝x（18－x） C、y＝x（40－2x） D、y＝2x（40－x）

查看试题解析
9. 下列事件是必然事件的为（）

A、明天早上会下雨 B、任意一个三角形，它的内角和等于 $180 °$ C、踯一枚硬币，正面朝上 D、打开电视机，正在播放“新闻联播”

查看试题解析
10. 如图，抛物线y=ax²+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(-1，0)，其部分图象如图所示下列结论：①4ac＜b²；②方程ax²+bx+c=0的两个根是 $x_{1} = - 1 ， x_{2} = 3$ ；③3a+c＞0；④当y＞0时，x的度值范围是-1＜x＜4；⑤当x<0时，y随x的增大而增大．其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 一元二次方程3x²﹣6x＝0的根是．

查看试题解析
12. 如图，⊙C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为(0，3)，M是第三象限内弧OB上一点，∠BMO＝120°，则⊙C的半径为.

查看试题解析
13. 若方程 $x^{2} - 4 x + m = 0$ 有两个相等的实数根，则m= ．

查看试题解析
14. 如图，四边形ABCD内接于⊙O，∠A=105°，则∠BOD= ．

查看试题解析
15. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是 $⊙ O$ 的切线，切点为A， $B C$ 交 $⊙ O$ 于点D，点E是 $A C$ 的中点．若 $⊙ O$ 的半径为2， $∠ B = 5 0^{∘}$ ， $A C = 4.8$ ，则阴影部分的面积为．

查看试题解析
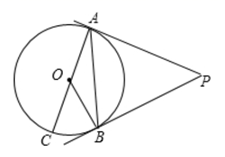
16. 如图，PA，PB是⊙O是切线，A，B为切点，AC是⊙O的直径，若∠BAC=25°，则∠P=度．

查看试题解析
17. 如图，有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就到达警戒线CD，这时水面宽度为10米．若洪水到来时，水位以每小时0.2米的速度上升小时水位能由正常水位到达拱桥顶．

查看试题解析

三、解答题

18. 解下列方程：

(1)、x²﹣2x+1＝25．

(2)、3x（x - 1）= 2（x - 1）．

查看试题解析
19. 先化简，再求值．
$\frac{a - 2}{a^{2} - 3 a} \div (a + 3 + \frac{5}{a - 3})$ ，请从一元二次方程 $a^{2} - 7 a + 12 = 0$ 的两个根中选择一个你喜欢的求值．

查看试题解析
20. 如图，有四张反面完全相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形，将四张纸牌洗匀后正面朝下随机放在桌面上，先从四张纸牌中随机摸出一张，不放回，再从剩下的纸牌中随机摸出一张.请用“列表法”或“树状图法”求模出的两张牌既是轴对称图形又是中心对称图形的概率（纸牌用A、B、C、D表示）.

查看试题解析
21. 如图，正三角形 $A B C$ 的边长为 $a ， D ， E ， F$ 分别为 $B C ， C A ， A B$ 的中点，以 $A ， B ， C$ 三点为圆心， $\frac{a}{2}$ 长为半径作圆，求图中阴影部分的面积．

查看试题解析
22. 一块长5米、宽4米的地毯如图所示，为了美观设计了两横、两纵的配色条纹（图中阴影部分），已知配色条纹的宽度相同，所占面积是整个地毯面积的 $\frac{17}{80}$ .

(1)、求配色条纹的宽度；

(2)、如果地毯配色条纹部分每平方米造价200元，其余部分每平方米造价100元，求地毯的总造价.

查看试题解析
23. 已知关于x的一元二次方程x²+（m+3）x+m+1=0．

(1)、求证：无论m取何值，原方程总有两个不相等的实数根；

(2)、若x₁ ， x₂是原方程的两根，且 $| x_{1} - x_{2} | = 2 \sqrt{2}$ ，求m的值，并求出此时方程的两根．

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径，C为 $⊙ O$ 上一点， $∠ D C A = ∠ B$ ．

(1)、求证： $C D$ 是 $⊙ O$ 的切线．

(2)、若 $D E ⊥ A B$ ，垂足为E， $D E$ 交 $A C$ 于点F，求证： $△ D C F$ 是等腰三角形．

查看试题解析
25. 如图，抛物线y=x²+bx+c与x轴交于A（一1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，m）.

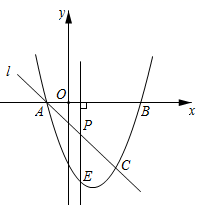(1)、求抛物线的解析式.

(2)、点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标.

(3)、点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由.

查看试题解析