辽宁省本溪市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 在﹣3,﹣1,0,2这四个数中,最小的数是( )A、﹣3 B、﹣1 C、0 D、22. 一个几何体如图所示,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算中,计算正确的是( )A、 B、 C、 D、4. 下列图形中,既是中心对称图形又是抽对称图形的是( )A、
3. 下列运算中,计算正确的是( )A、 B、 C、 D、4. 下列图形中,既是中心对称图形又是抽对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、26. 下列说法正确的是( )A、“打开电视机,正在播放《新闻联播》”是必然事件 B、“明天下雨概率为0.5”,是指明天有一半的时间可能下雨 C、一组数据“6,6,7,7,8”的中位数是7,众数也是7 D、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同.方差分别是 , ,则甲的成绩更稳定7. 下列说法正确的是( )A、函数 的图象是过原点的射线 B、直线 经过第一、二、三象限 C、函数 ,y随x增大而增大 D、函数 ,y随x增大而减小8. 如图,在 中, ,分别以点A,B为圆心,大于 的长为半径画弧,两弧相交于点M和点N,作直线 分别交 、 于点D和点E,若 ,则 的度数是( )
5. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、26. 下列说法正确的是( )A、“打开电视机,正在播放《新闻联播》”是必然事件 B、“明天下雨概率为0.5”,是指明天有一半的时间可能下雨 C、一组数据“6,6,7,7,8”的中位数是7,众数也是7 D、甲、乙两人在相同的条件下各射击10次,他们成绩的平均数相同.方差分别是 , ,则甲的成绩更稳定7. 下列说法正确的是( )A、函数 的图象是过原点的射线 B、直线 经过第一、二、三象限 C、函数 ,y随x增大而增大 D、函数 ,y随x增大而减小8. 如图,在 中, ,分别以点A,B为圆心,大于 的长为半径画弧,两弧相交于点M和点N,作直线 分别交 、 于点D和点E,若 ,则 的度数是( ) A、 B、 C、 D、9. 如图,在中, , , , 将绕原点O逆时针旋转90°,则旋转后点A的对应点的坐标是( )
A、 B、 C、 D、9. 如图,在中, , , , 将绕原点O逆时针旋转90°,则旋转后点A的对应点的坐标是( ) A、 B、 C、 D、10. 如图,在中, , , E是AB的中点,过点E作AC和BC的垂线,垂足分别为点E和点F,四边形CDEF沿着CA方向匀速运动,当点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与重叠部分面积为S,则下列图象能大致反应S与t之间函数关系的是( )
A、 B、 C、 D、10. 如图,在中, , , E是AB的中点,过点E作AC和BC的垂线,垂足分别为点E和点F,四边形CDEF沿着CA方向匀速运动,当点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与重叠部分面积为S,则下列图象能大致反应S与t之间函数关系的是( )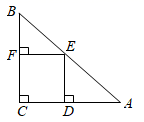 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
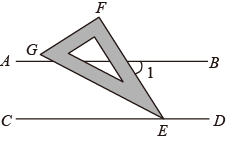
11. 截止到2021年12月1日,全国累计新冠疫苗接种超2510000000剂次,用科学记数法表示2510000000这个数,应记作 .12. 分解因式: .13. 关于x的方程有两个不相等的实数根,则m的取值范围是 .14. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.
 15. 小明上学经过两个路口,如果每个路口可直接通过或需等待的可能性相等,那么小明上学时在这两个路口都直接通过的概率为.16. 三个顶点的坐标分别为 , , , 以原点为位似中心,相似比为 , 将缩小,则点B的对应点的坐标是.17. 如图,在平面直角坐标系中,菱形ABCD的边轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数的图象同时经过顶点C,D.若点C的横坐标为5, , 则k的值为 .
15. 小明上学经过两个路口,如果每个路口可直接通过或需等待的可能性相等,那么小明上学时在这两个路口都直接通过的概率为.16. 三个顶点的坐标分别为 , , , 以原点为位似中心,相似比为 , 将缩小,则点B的对应点的坐标是.17. 如图,在平面直角坐标系中,菱形ABCD的边轴,垂足为E,顶点A在第二象限,顶点B在y轴正半轴上,反比例函数的图象同时经过顶点C,D.若点C的横坐标为5, , 则k的值为 . 18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ . 则其中正确的结论有 .
18. 如图,在正方形ABCD的对角线AC上取一点E,使得 , 连接BE并延长BE到F,使 , BF与CD相交于点H,若 , 有下列结论:①;②;③;④ . 则其中正确的结论有 .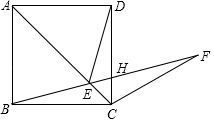
三、解答题
-
19. 先化简,再求值: ,其中 .20. “大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
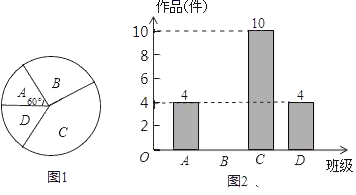 (1)、王老师采取的调查方式是(填“普查”或“抽样调查”),王老师所调查的4个班共征集到作品件,并补全条形统计图;(2)、在扇形统计图中,表示C班的扇形周心角的度数为;(3)、如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)21. 某校九年级有三个班,其中九年一班和九年二班共有105名学生,在期末体育测试中,这两个班级共有79名学生满分,其中九年一班的满分率为70%,九年二班的满分率为80%.(1)、求九年一班和九年二班各有多少名学生.(2)、该校九年三班有45名学生,若九年级体育成绩的总满分率超过75%,求九年三班至少有多少名学生体育成绩是满分.22. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 .
(1)、王老师采取的调查方式是(填“普查”或“抽样调查”),王老师所调查的4个班共征集到作品件,并补全条形统计图;(2)、在扇形统计图中,表示C班的扇形周心角的度数为;(3)、如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)21. 某校九年级有三个班,其中九年一班和九年二班共有105名学生,在期末体育测试中,这两个班级共有79名学生满分,其中九年一班的满分率为70%,九年二班的满分率为80%.(1)、求九年一班和九年二班各有多少名学生.(2)、该校九年三班有45名学生,若九年级体育成绩的总满分率超过75%,求九年三班至少有多少名学生体育成绩是满分.22. 如图,在平面直角坐标系中, 的斜边 在 轴上,坐标原点是 的中点, , ,双曲线 经过点 . (1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.23. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: 1.414, =1.732).
(1)、求 ;(2)、直线 与双曲线 在第四象限交于点 .求 的面积.23. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据: 1.414, =1.732).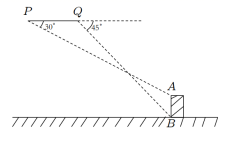 24. 某服装厂批发应季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示.
24. 某服装厂批发应季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示. (1)、直接写出y与x的函数关系式;(2)、若每件T恤衫的成本价是45元,当件(x为正整数)时,服装厂如果想获得8000元利润,求一次批发多少件时所获利润为8000元?25. 在正方形ABCD中,过点B作直线l,点E在直线l上,连接CE,DE,其中 , 过点C作于点F,交直线l于点H.
(1)、直接写出y与x的函数关系式;(2)、若每件T恤衫的成本价是45元,当件(x为正整数)时,服装厂如果想获得8000元利润,求一次批发多少件时所获利润为8000元?25. 在正方形ABCD中,过点B作直线l,点E在直线l上,连接CE,DE,其中 , 过点C作于点F,交直线l于点H. (1)、当直线l在如图①的位置时
(1)、当直线l在如图①的位置时①请直接写出与之间的数量关系 .
②请直接写出线段BH,EH,CH之间的数量关系 .
(2)、当直线l在如图②的位置时,请写出线段BH,EH,CH之间的数量关系并证明;(3)、已知 , 在直线l旋转过程中当时,请直接写出EH的长.26. 如图1,直线AB与x轴,y轴分别交于A,B两点,点C在x轴负半轴上,这三个点的坐标分别为A(4,0),B(0,4),C(−1,0) .
 (1)、请求出直线AB的解析式;(2)、连接BC,若点E是线段AC上的一个动点(不与A,C重合),过点E作EF//BC交AB于点F,当△BEF的面积是时,求点E的坐标;(3)、如图2,将点B向右平移1个单位长度得到点D,在x轴上存在动点P,若∠DCO+∠DPO=∠α,当tan∠α=4时,请直接写出点P的坐标.
(1)、请求出直线AB的解析式;(2)、连接BC,若点E是线段AC上的一个动点(不与A,C重合),过点E作EF//BC交AB于点F,当△BEF的面积是时,求点E的坐标;(3)、如图2,将点B向右平移1个单位长度得到点D,在x轴上存在动点P,若∠DCO+∠DPO=∠α,当tan∠α=4时,请直接写出点P的坐标.