吉林省延边州2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 下列四个图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,属于必然事件的是( )A、三角形的外心到三边的距离相等 B、某射击运动员射击一次,命中靶心 C、任意画一个三角形,其内角和是 180° D、抛一枚硬币,落地后正面朝上3. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、114. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
2. 下列事件中,属于必然事件的是( )A、三角形的外心到三边的距离相等 B、某射击运动员射击一次,命中靶心 C、任意画一个三角形,其内角和是 180° D、抛一枚硬币,落地后正面朝上3. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、114. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )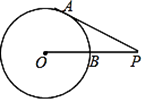 A、3 B、3 C、6 D、95. 如图,是半圆O的直径,C为半圆O上的一点,连接为上的点,连接若 , 则的度数是( )
A、3 B、3 C、6 D、95. 如图,是半圆O的直径,C为半圆O上的一点,连接为上的点,连接若 , 则的度数是( )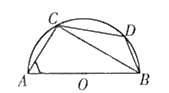 A、 B、 C、 D、6. 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ) A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
7. 方程 的根是 .8. 点P(﹣4,6)与Q(2m,﹣6)关于原点对称,则m= .9. 已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是.10. 点是抛物线与x轴的一个交点,则的值是 .11. 在一个不透明的盒子中装有2个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为 , 则黄球的个数为 .12. 学校组织一次乒乓球赛,要求每两队之间都要比赛一场.若共赛了28场,设有个球队参赛,根据题意列出x满足的关系式为 .13. 是的内接正六边形一边,点P是优弧上的一点(点P不与点A,B重合)且 , 与交于点C,则的度数为 .
 14. 如图,在菱形中,对角线和交于点O,分别以A,C为圆心, , 为半径画圆弧,交菱形各边于点E,F,G,H.若 , , 则图中阴影部分的面积是 . (结果保留)
14. 如图,在菱形中,对角线和交于点O,分别以A,C为圆心, , 为半径画圆弧,交菱形各边于点E,F,G,H.若 , , 则图中阴影部分的面积是 . (结果保留)
三、解答题
-
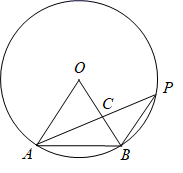
15. 解方程: .16. 不透明的口袋里装有2个红球和2个黄球(除颜色不同外,其它都相同).现进行两次摸球活动,第一次随机摸出一个小球后不放回,第二次再随机摸出一个小球,请用树状图或列表法,求两次摸出的都是红球的概率.17. 某地区2019年投入教育经费2500万元,2021年投入教育经费3025万元.求2019年至2021年该地区投入教育经费的年平均增长率.18. 如图,⊙O中, ,∠C=75°,求∠A的度数.
 19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为、、 .
19. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为、、 .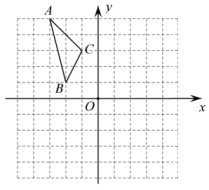 (1)、画出将关于点O对称的图形;(2)、写出点、、的坐标.20. 如图,在平面直角坐标系中,抛物线过点 , .
(1)、画出将关于点O对称的图形;(2)、写出点、、的坐标.20. 如图,在平面直角坐标系中,抛物线过点 , .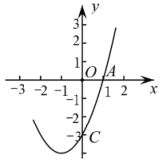 (1)、求这条抛物线的解析式;(2)、当时,x的取值范围是 .21. 如图,在等腰△ABC中,AB=AC,点D是BC上一点,以BD为直径的⊙O过点A,连接AD,∠CAD=∠C.
(1)、求这条抛物线的解析式;(2)、当时,x的取值范围是 .21. 如图,在等腰△ABC中,AB=AC,点D是BC上一点,以BD为直径的⊙O过点A,连接AD,∠CAD=∠C.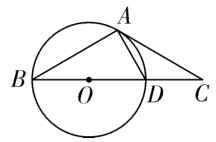 (1)、求证:AC是⊙O的切线;(2)、若AC=4,则⊙O的半径长为 .22. 如图,将小球从地面击出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系: .
(1)、求证:AC是⊙O的切线;(2)、若AC=4,则⊙O的半径长为 .22. 如图,将小球从地面击出,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系: . (1)、小球的飞行高度能否达到?如果能,需要多少飞行时间?(2)、直接写出小球从飞出到落地需要的时间;(3)、小球的飞行高度能否达到?为什么?23. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
(1)、小球的飞行高度能否达到?如果能,需要多少飞行时间?(2)、直接写出小球从飞出到落地需要的时间;(3)、小球的飞行高度能否达到?为什么?23. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:x(元)
15
20
30
…
y(袋)
25
20
10
…
若日销售量y是销售价x的一次函数,试求:
(1)、日销售量y(袋)与销售价x(元)的函数关系式;(2)、假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?24. 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.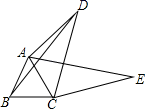 (1)、求证:AE=BD;(2)、若∠ADC=30°,AD=3,BD=4 .求CD的长.25. 如图①,在中, , , 点D,E分别在边 , 上,且 , 此时 , 成立.
(1)、求证:AE=BD;(2)、若∠ADC=30°,AD=3,BD=4 .求CD的长.25. 如图①,在中, , , 点D,E分别在边 , 上,且 , 此时 , 成立.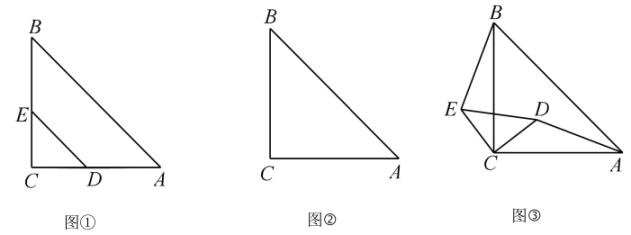 (1)、将绕点C逆时针旋转时,在图②中补充图形,并直接写出的长度;(2)、当绕点C逆时针旋转一周的过程中,与的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)、将绕点C逆时针旋转一周的过程中,当A,D,E三点在同一条直线上时,请直接写出的长度.26. 在平面直角坐标系中,抛物线过点且与y轴交于点B,抛物线的顶点为C.点P为该抛物线上一动点(不与C重合),设点P的横坐标为m.
(1)、将绕点C逆时针旋转时,在图②中补充图形,并直接写出的长度;(2)、当绕点C逆时针旋转一周的过程中,与的数量关系和位置关系是否仍然成立?若成立,请你利用图③证明,若不成立请说明理由;(3)、将绕点C逆时针旋转一周的过程中,当A,D,E三点在同一条直线上时,请直接写出的长度.26. 在平面直角坐标系中,抛物线过点且与y轴交于点B,抛物线的顶点为C.点P为该抛物线上一动点(不与C重合),设点P的横坐标为m.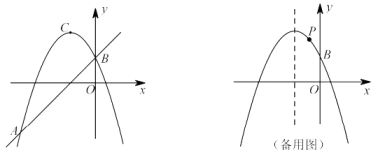 (1)、抛物线对应的解析式 , 顶点C的坐标;(2)、将该抛物线沿y轴向下平移2个单位,点P的对应点为 , 若 , 求的面积S;(3)、当点C、P到直线的距离相等时,求m的值;(4)、当点P在对称轴右侧时,连接 , 以为边作正方形 , 当点D恰好落在该抛物线的对称轴上时,直接写出点P的坐标.
(1)、抛物线对应的解析式 , 顶点C的坐标;(2)、将该抛物线沿y轴向下平移2个单位,点P的对应点为 , 若 , 求的面积S;(3)、当点C、P到直线的距离相等时,求m的值;(4)、当点P在对称轴右侧时,连接 , 以为边作正方形 , 当点D恰好落在该抛物线的对称轴上时,直接写出点P的坐标.