黑龙江省齐齐哈尔市龙沙区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、2 D、2. 下列图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列事件中,属于不可能事件的是( )A、掷一校骰子,朝上一面的点数为5 B、任意画一个三角形,它的内角和是178° C、某个数的相反数等于它本身 D、在纸上画两条直线,这两条直线互相垂直4. 若m是方程的一个根,则的值为( )A、2019 B、2020 C、2021 D、20225. 如图,正六边形内接于圆O,半径为4,则这个正六边形的边心距为( )
3. 下列事件中,属于不可能事件的是( )A、掷一校骰子,朝上一面的点数为5 B、任意画一个三角形,它的内角和是178° C、某个数的相反数等于它本身 D、在纸上画两条直线,这两条直线互相垂直4. 若m是方程的一个根,则的值为( )A、2019 B、2020 C、2021 D、20225. 如图,正六边形内接于圆O,半径为4,则这个正六边形的边心距为( ) A、2 B、 C、 D、6. 如图,在平行四边形中,点M为的中点,与相交于点N,若已知 , 那么等于( )
A、2 B、 C、 D、6. 如图,在平行四边形中,点M为的中点,与相交于点N,若已知 , 那么等于( ) A、6 B、9 C、12 D、37. 若抛物线与x轴没有交点,则m的取值范围是( )A、 B、 C、 D、8. 在同一平面直角坐标系中,函数与的图象可能是( ).A、
A、6 B、9 C、12 D、37. 若抛物线与x轴没有交点,则m的取值范围是( )A、 B、 C、 D、8. 在同一平面直角坐标系中,函数与的图象可能是( ).A、 B、
B、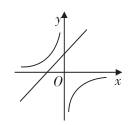 C、
C、 D、
D、 9. 如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B'的坐标为( )
9. 如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B'的坐标为( ) A、( , ) B、(-1,) C、(- , ) D、(- , )10. 已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤ , 其中正确的结论有( )
A、( , ) B、(-1,) C、(- , ) D、(- , )10. 已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤ , 其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 某商场一月份利润为100万元,三月份的利润为121万元,则该商场二、三月利润的平均增长率为x,则可列出方程为 .12. 如图,在中,D是线段上的一点(不与点A,B重合),连接 . 请添加一个条件使与相似,这个条件可以是(写出一个即可).
 13. 已知一个圆锥的侧面展开图是一个圆心角为120°,面积为12的扇形,则这个圆锥的高是cm.14. 若关于x的一元二次方程有实数根,则实数k的取值范围是 .15. 如图,反比例函数的图象经过对角线的交点P,已知点A,C,D在坐标轴上, , 的面积为8,则 .
13. 已知一个圆锥的侧面展开图是一个圆心角为120°,面积为12的扇形,则这个圆锥的高是cm.14. 若关于x的一元二次方程有实数根,则实数k的取值范围是 .15. 如图,反比例函数的图象经过对角线的交点P,已知点A,C,D在坐标轴上, , 的面积为8,则 . 16. 如图,在中, , , , 点E,F分别在边 , 上,沿所在的直线折叠 , 使点C的对应点D恰好落在边上.若和相似,则的长为 .
16. 如图,在中, , , , 点E,F分别在边 , 上,沿所在的直线折叠 , 使点C的对应点D恰好落在边上.若和相似,则的长为 . 17. 二次函数的图象如图所示,点位于坐标原点,点 , , , …,在y轴的正半轴上,点 , , , …,在二次函数位于第一象限的图象上, , , …,都是直角顶点在抛物线上的等腰直角三角形,则的斜边长为 .
17. 二次函数的图象如图所示,点位于坐标原点,点 , , , …,在y轴的正半轴上,点 , , , …,在二次函数位于第一象限的图象上, , , …,都是直角顶点在抛物线上的等腰直角三角形,则的斜边长为 .
三、解答题
-
18. 计算:19. 解方程:(1)、(2)、20. 为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
 (1)、填空:样本容量为 , a=;(2)、把频数分布直方图补充完整;(3)、若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.21. 如图,以点为圆心,长为直径作圆,在上取一点 , 延长至点 , 连接 , , 过点作交的延长线于点 .
(1)、填空:样本容量为 , a=;(2)、把频数分布直方图补充完整;(3)、若从该地随机抽取1名学生,估计这名学生身高低于160cm的概率.21. 如图,以点为圆心,长为直径作圆,在上取一点 , 延长至点 , 连接 , , 过点作交的延长线于点 . (1)、求证:是的切线;(2)、若 , , 求的长.22. 如图一次函数的图象与坐标轴相交于点和点B,与反比例函数的图象相交于点 .
(1)、求证:是的切线;(2)、若 , , 求的长.22. 如图一次函数的图象与坐标轴相交于点和点B,与反比例函数的图象相交于点 .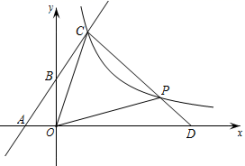 (1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接并延长,交x轴正半轴于点D,若时,求的面积;(3)、在(2)的条件下,在y轴上是否存在点Q,使的值最小,若存在请直接写出的最小值,若不存在请说明理由.23. 等腰直角三角形中, , 为的角平分线,交于点E,点D为的中点,连结交于点G,过点C作 , 垂足为点F,交于点H.
(1)、求出一次函数与反比例函数的解析式;(2)、若点P是反比例函数图象上的一点,连接并延长,交x轴正半轴于点D,若时,求的面积;(3)、在(2)的条件下,在y轴上是否存在点Q,使的值最小,若存在请直接写出的最小值,若不存在请说明理由.23. 等腰直角三角形中, , 为的角平分线,交于点E,点D为的中点,连结交于点G,过点C作 , 垂足为点F,交于点H. (1)、如图1,与的数量关系为;的值为;(2)、如图2,以点C为位似中心,将做位似交换,得到 , 使与的相似比为 , 与、的交点分别为 , , 隐去线段 , 试求的值;(3)、如图3,将(2)中的等腰直角三角形改为等腰三角形, , 且其他条件不变,
(1)、如图1,与的数量关系为;的值为;(2)、如图2,以点C为位似中心,将做位似交换,得到 , 使与的相似比为 , 与、的交点分别为 , , 隐去线段 , 试求的值;(3)、如图3,将(2)中的等腰直角三角形改为等腰三角形, , 且其他条件不变,①的值为;
②若 , 直接写出的面积 .
24. 如图,抛物线与x轴交于 , 两点,与y轴交于点 , 抛物线的顶点为D,连接 , P为线段上的一个动点(P不与B、C重合),过点P作轴,交抛物线于点F,交x轴于点G. (1)、求抛物线的解析式;(2)、当时,求点P的坐标;(3)、连接、、、 , 当的面积等于的面积时(点F与点D不重合),求点P的坐标;(4)、在(3)的条件下,在y轴上,是否存在点Q,使为等腰三角形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、当时,求点P的坐标;(3)、连接、、、 , 当的面积等于的面积时(点F与点D不重合),求点P的坐标;(4)、在(3)的条件下,在y轴上,是否存在点Q,使为等腰三角形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.