河北省保定市莲池区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $x^{2} - 6 x = 0$ 的解是（）

A、6 B、0 C、0或6 D、-6或0

查看试题解析
2. 用配方法解方程 $x^{2} - 4 x - 4 = 0$ ，则方程可变形为（）

A、 ${(x + 2)}^{2} = 8$ B、 ${(x - 2)}^{2} = 0$ C、 ${(x - 1)}^{2} = 5$ D、 ${(x - 2)}^{2} = 8$

查看试题解析
3. 由6个大小相同的正方体搭成的几何体如图所示，则它的三种视图中，面积一样的是（）

A、主视图与俯视图 B、主视图与左视图 C、俯视图与左视图 D、主视图、左视图和俯视图

查看试题解析
4. 养鱼池养了同一品种的鱼，要大概了解养鱼池中的鱼的数量，池塘的主人想出了如下的办法：“他打捞出80尾鱼，做了标记后又放回了池塘，过了三天，他又捞了一网，发现捞起的90尾鱼中，带标记的有6尾．”你认为池塘主的做法（）

A、有道理，池中大概有1200尾鱼 B、无道理 C、有道理，池中大概有7200尾鱼 D、有道理，池中大概有1280尾鱼

查看试题解析
5. 下图是文易同学答的试卷，文易同学应得（）

A、40分 B、60分 C、80分 D、100分

查看试题解析
6. 一小球从斜坡的顶端沿斜坡向下滚落到斜坡底端，行了100米，下落的铅直高度为50米，则该斜坡的坡度为（）

A、30° B、 $1 ： \sqrt{3}$ C、 $\sqrt{3}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图，作 $R t △ A B C$ ， $∠ C = 90 °$ ， $B C = 2 A C$ ；以A为圆心，以AC长为半径画弧，交斜边AB与点D；以B为圆心，以BD长为半径画弧，交BC与点E．若 $B C = 6$ ，则 $C E =$ （）

A、 $9 - 3 \sqrt{5}$ B、 $3 \sqrt{5} - 6$ C、 $3 \sqrt{5} - 3$ D、 $3 \sqrt{5} - 1$

查看试题解析
8. 某公司今年10月的营业额为2500万元，按计划第十二月的总营业额要达到9100万元，求该公司11；12两个月营业额的月均增长率，设该公司11，12两个月营业额的月均增长率为 $x$ ，则根据题意可列的方程为（）

A、 $x = \frac{\frac{9100 - 2500}{2500}}{2} \times 100 %$ B、 $9100 {(1 - x)}^{2} = 2500$ C、 $2500 {(1 + x)}^{2} = 9100$ D、 $9100 {(1 + x)}^{2} = 2500$

查看试题解析
9. 如图，D，E分别是 $△ A B C$ 的边AB，AC的中点，CD与BE交于点O，则 $S_{△ C O E} ： S_{△ B O C}$ 的值为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图，在四边形ABCD中， $A D ∥ B C$ ， $∠ A B C = 90 °$ ， O为对角线BD的中点， $O A = 2$ ， $B C = 5$ ， $C D = 3$ ，则 $t a n ∠ D C B$ 等于（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
11. 如图，反比例函数 $y = - \frac{a}{x}$ 与 $y = \frac{6}{x}$ 的图像上分别有一点A，B，且 $A B ∥ x$ 轴， $A D ⊥ x$ 轴于D， $B C ⊥ x$ 轴于C，若矩形ABCD的面积为8，则 $a =$ （）

A、-2 B、-6 C、2 D、6

查看试题解析
12. 在如图所示的网格中，以点O为位似中心，四边形 $A B C D$ 的位似图形是（）

A、四边形 $N P M Q$ B、四边形 $N P M R$ C、四边形 $N H M Q$ D、四边形 $N H M R$

查看试题解析
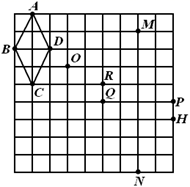13. 已知点 $(- 3 ， a)$ ， $(3 ， b)$ ， $(- 5 ， c)$ 均在反比例函数 $y = \frac{| k | + 1}{x}$ 的图像上，则有（）

A、 $a < b < c$ B、 $c < b < a$ C、 $b < a < c$ D、 $a < c < b$

查看试题解析
14. 二次函数 $y = {(x + k)}^{2} + h$ 的图象与x轴的交点的横坐标分别为-1和3，则 $y = {(x + k + 2)}^{2} + h$ 的图象与x轴的交点的横坐标分别为（）

A、-3和1 B、1和5 C、-3和5 D、3和5

查看试题解析
15. 点 $A (a ， b)$ 在反比例函数 $y = \frac{9}{x}$ 上的点图象上，且a，b是关于的一元二次方程 $x^{2} - 6 x + m = 0$ 的两根，则点A坐标是（）

A、（1，9） B、 $(2 ， \frac{9}{2})$ C、（3，3） D、（-3，-3）

查看试题解析
16. 对于题目“抛物线 $l_{1}$ ： $y = {(x - 1)}^{2} - 4 (- 1 < x \leq 4)$ 与直线 $l_{2}$ ： $y = m$ 只有一个交点，则整数m的值有几个”；你认为m的值有（）

A、3个 B、5个 C、6个 D、7个

查看试题解析

二、填空题

17. 若 $3 x = 2 y (y \neq 0)$ ，则 $\frac{x - y}{y} =$ ．

查看试题解析
18. 已知抛物线 $y = x^{2} + m x + m - 2$ 与x轴的两个交点在点（1，0）两旁，则m的取值范围是．

查看试题解析
19. 如图，点O是正方形ABCD的称中心O，互相垂直的射线OM，ON分别交正方形的边AD，CD于E，F两点，连接EF；已知 $A D = 2$ ．

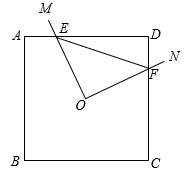(1)、以点E，O，F，D为顶点的图形的面积为；

(2)、线段EF的最小值是．

查看试题解析

三、解答题

20. 如图，已知，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 30 °$ ．将 $△ A B C$ 绕点A逆时针旋转一个 $α$ 角 $(0 ° < α < 180 °)$ 至 $△ A D E$ 位置，连接BD，CE交于点F．

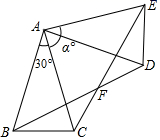(1)、求证： $△ A B D ≌ △ A C E$

(2)、若四边形ABFE为菱形，求 $α$ 的值；

(3)、在（2）的条件下，若 $A B = 2$ ，直接写出CF的值．

查看试题解析
21. 已知关于x的一元二次方程： $2 x^{2} + 4 x + k = 0$ ．

(1)、当 $k = 1$ 时，解方程：

(2)、若 $2 x^{2} + 4 x + k = 0$ 的一个解是 $x = - 1$ ，求k；

(3)、若抛物线 $y = 2 x^{2} + 4 x + k$ 与x轴无交点，试确定k的取值范围．

查看试题解析
22. 九年级十班的甲、乙两位同学练习百米赛跑；操场上从内道到外道，标有1，2，3，4四个跑道．他们抽签占跑道．

(1)、若甲抽到2道，则乙抽到3道的概率是；

(2)、请列表或画树状图求甲、乙在相邻跑道的概率．

查看试题解析
23. 如图，从甲楼AB的楼顶A，看乙楼CD的楼顶C，仰角为30°，看乙楼（CD）的楼底D，俯角为60°；已知甲楼的高AB=40m．求乙楼CD的高度，（结果精确到1m）

查看试题解析
24. 如图，在平面直角坐标系中，正比例函数 $y = k x$ 的图象 $L_{1}$ 与反比例函数 $y = \frac{6 - k}{x}$ 的图象 $L_{2}$ 的两个交点分别为 $A (1 ， a)$ ， $B (m ， n)$ ．

(1)、则 $a =$ ， $m =$ ， $n =$ ；

(2)、求双曲线 $L_{2}$ 的函数表达式；

(3)、若 $C (3 ， c)$ 在双曲线 $L_{2}$ 上，过点 $C$ 作 $C D ⊥ x$ 轴，垂足为D．求四边形 $A O D C$ 的面积；

(4)、若 $k x > \frac{6 - k}{x}$ ，请根据图象，直接写出 $x$ 的取值范围．

查看试题解析
25. 我市某卖场的一专营柜台，专营一种电器，每台进价60元．调查发现，当销售价80元时，平均每月能售出1000台；当销售价每涨1元时，平均每月能少售出10台；该柜台每月还需要支出20000元的其它费用，为了防止不正当竞争，稳定市场，市物价局规定：“出售时不得低于80元/台，又不得高于180元/台”．设售价为 $x$ 元/台时，月平均销售量为y台，月平均利润为w元．
注：月利润=月总售价-月总进价-其它费用，或月利润=月总销售量×单台利润-其它费用．

(1)、当 $x = 85$ 元/台时， $y =$ 台， $w =$ 元；

(2)、求y与x的函数关系式，w与x的函数关系式（写出x的取值范围）；

(3)、每台售价多少元时，月销售利润最高，最高为多少元；

(4)、因为新品快要上市了，卖场既要想使该种电器平均每月获利7000元，又想要减少库存，售价应定为多少元．

查看试题解析
26. 如图，已知矩形ABCD， $A B = \sqrt{5}$ ， $B C = 6$ ．点P从B出发，以1/s的速度沿边BC运动，（点P不与点C重合），连接AP，作 $P E ⊥ A P$ ，交矩形ABCD的边于N，设点P的运动时间为 $t s (t > 0)$

(1)、 $t = \frac{1}{2}$ 时，则 $C N =$ ；

(2)、若 $A P ⊥ B D$ ，求t的值；

(3)、当N在CD边上时，且 $t a n ∠ A N P = \frac{\sqrt{5}}{5}$ ，求 $△ P C N$ 的面积；

(4)、当N在CD边上时，直接写出t的取值范围．

查看试题解析