河北省保定市定州市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点 $(2 ， 3)$ 关于原点对称的点的坐标是（）

A、 $(3 ， 2)$ B、 $(2 ， - 3)$ C、 $(- 2 ， - 3)$ D、 $(- 3 ， - 2)$

查看试题解析
3. 在下列各点中，抛物线y＝3x²经过点（）

A、（0，﹣1） B、（0，0） C、（0，1） D、（0，2）

查看试题解析
4. 下列图形中，一定相似的是（　　）

A、两个正方形 B、两个菱形 C、两个直角三角形 D、两个等腰三角形

查看试题解析
5. 反比例函数y＝ $\frac{k}{x}$ 的图象经过点（﹣3，1），则下列说法错误的是（）

A、k＝﹣3 B、函数的图象在第二、四象限 C、函数图象经过点（3，﹣1） D、当x＞0时，y随x的增大而减小

查看试题解析
6. 一元二次方程 $x^{2} - 8 x - 1 = 0$ 配方后可变形为（）

A、 ${(x + 4)}^{2} = 17$ B、 ${(x + 4)}^{2} = 15$ C、 ${(x - 4)}^{2} = 17$ D、 ${(x - 4)}^{2} = 15$

查看试题解析
7. 如图，点O是△ABC的内心，∠A＝62°，则∠BOC＝（）

A、59° B、31° C、124° D、121°

查看试题解析
8. 如图，已知Rt△ABC中，∠C＝90°，∠A＝30°，AC＝6，以点B为圆心，3为半径作⊙B ，则点C与⊙B的位置关系是（）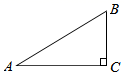

A、点C在⊙B内 B、点C在⊙B上 C、点C在⊙B外 D、无法确定

查看试题解析
9. 若关于x的一元二次方程（m+1）x²-2x+1=0有实数根，则实数m的取值范围是（）

A、m≥0 B、m≤0 C、m≠1 D、m≤0且m≠-1

查看试题解析
10. 如图，已知△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的 $\frac{4}{9}$ ，则AO：AD的值为（）

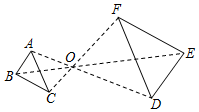A、2：3 B、2：5 C、4：9 D、4：13

查看试题解析
11. 如图，正方形 $A B C D$ 的边长为4，以点A为圆心， $A D$ 为半径画圆弧 $D E$ 得到扇形 $D A E$ （阴影部分，点E在对角线 $A C$ 上）.若扇形 $D A E$ 正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（）

A、 $\sqrt{2}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
12. 已知点A（x₁ ， y₁），B（x₂ ， y₂）是双曲线 $y = - \frac{3}{x}$ 上的两点，若x₂＜0＜x₁ ，则有（）

A、0＜y₁＜y₂ B、0＜y₂＜y₁ C、y₂＜0＜y₁ D、y₁＜0＜y₂

查看试题解析
13. 如图，Rt△ABC中，∠C＝90°，AB＝10，AC＝8，E是边AC上一点，AE＝5，ED⊥AB ，垂足为点D ，则AD的长是（）

A、16 B、 $\frac{25}{4}$ C、6 D、4

查看试题解析
14. 如图，电路图上有4个开关A、B、C、D和1个小灯泡，在所有的元件和线路都正常的前提下．下列操作中，“小灯泡发光”这个事件是随机事件的是（）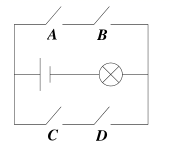

A、只闭合 $1$ 个开关 B、只闭合 $2$ 个开关 C、只闭合 $3$ 个开关 D、闭合 $4$ 个开关

查看试题解析
15. 如图，菱形OABC的顶点C的坐标为（3，4），顶点A在x轴的正半轴上．反比例函数 $y = \frac{k}{x}$ (x>0)的图象经过顶点B，则k的值为（）

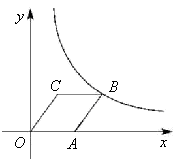A、12 B、20 C、24 D、32

查看试题解析
16. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，其对称轴为直线x＝﹣1，与x轴的交点为（x₁ ， 0）、（x₂ ， 0），其中0＜x₁＜1，有下列结论：①c＞0；②﹣3＜x₂＜﹣2；③a+b+c＜0；④b²﹣4ac＞0；⑤已知图象上点A（4，y₁），B（1，y₂），则y₁＞y₂ ．其中，正确结论的个数有（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

17. 已知正六边形的半径是3，则这个正六边形的边长是．

查看试题解析
18. 在一个不透明的口袋中，装有若干个红球和6个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率是0.3，则估计盒子中大约有红球。

查看试题解析
19.
如图，矩形ABCD的长AB=6cm，宽AD=3cm．O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线y=ax²经过C、D两点，则图中阴影部分的面积是 cm² ．

查看试题解析
20. 如图，⊙O的半径为2，点O到直线l的距离为4，过l上任一点P作⊙O的切线，切点为Q；若以PQ为边作正方形PQRS，则正方形PQRS的面积最小值为.

查看试题解析

三、解答题

21. 已知2是方程 $x^{2} - c = 0$ 的一个根，求常数 $c$ 的值及该方程的另一根．

查看试题解析
22. 如图，在平行四边形ABCD中，点E是AB的中点．CE和BD交于点O，若S_△_EOB＝1，求四边形AEOD的面积．

查看试题解析
23. 甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示. 游戏规定，转动两个转盘停止后，指针必须指到某一数字，否则重转．

(1)、请用树状图或列表法列出所有可能的结果；

(2)、若指针所指的两个数字都是方程x²-4x+3=0的解时，则甲获胜；若指针所指的两个数字都不是方程x²-4x+3=0的解时，则乙获胜．问他们两人谁获胜的概率大?请分析说明．

查看试题解析
24. 如图，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点，作△BCD的外接圆⊙O，CE是⊙O的直径，且CE与AB交于点G，DF∥EC交AC于点F．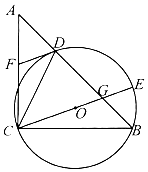

(1)、求证：DF为⊙O的切线；

(2)、若 $\frac{A D}{D G} = \frac{2}{3}$ ，AC＝5，求⊙O的半径长．

查看试题解析
25. 某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

(1)、直接写出y与x之间的函数关系式；

(2)、当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

(3)、若该网店每星期想要获得6480元的利润，求每件童装售价应为多少元？

查看试题解析
26. 如图，在平面直角坐标系中，直线AB和抛物线交于点A（-4，0），B（0，4），且点B是抛物线的顶点．

(1)、求直线AB和抛物线的解析式．

(2)、点P是直线上方抛物线上的一点，求当△PAB面积最大时点P的坐标．

(3)、M是直线AB上一动点，在平面直角坐标系内是否存在点N，使以O、B、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析