广东省珠海市香洲区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 垃圾分类一小步，低碳生活一大步，垃圾桶上常有以下四种垃圾分类标识的图案和文字说明，其中图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某学校九年级为庆祝建党一百周年举办“歌唱祖国”合唱比赛，用抽签的方式确定出场顺序．现有8根形状、大小完全相同的纸签，上面分别标有序号1、2、3、4、5、6、7、8．下列事件中是必然事件的是（）

A、一班抽到的序号小于6 B、一班抽到的序号为9 C、一班抽到的序号大于0 D、一班抽到的序号为7

查看试题解析
3. 反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象经过点A(﹣2，3)，则此图象一定经过下列哪个点（　　）

A、(3，2) B、(﹣3，﹣2) C、(﹣3，2) D、(﹣2，﹣3)

查看试题解析
4. 下列关于x的一元二次方程中，有两个相等的实数根的方程是（）

A、 $x^{2} + 4 = 0$ B、 $x^{2} - 2 x + 1 = 0$ C、 $x^{2} - x - 3 = 0$ D、 $x^{2} + 2 x = 0$

查看试题解析
5. 抛物线 $y = (x + 1)^{2} - 2$ 的顶点坐标是（）

A、（－1，2） B、（－1，－2） C、（1，－2） D、（1，2）

查看试题解析
6. 如图，在Rt△ABC中，∠ACB＝90°，AB＝5 cm，BC＝3 cm，△ABC绕AC所在直线旋转一周，所形成的圆锥侧面积等于（）

A、4πcm² B、8πcm² C、12πcm² D、15πcm²

查看试题解析
7. 如图，在平面直角坐标系xOy中，点A（0，3），点B（2，1），点C（2，－3）．则经画图操作可知：△ABC的外接圆的圆心坐标是（）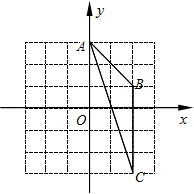

A、（－2，－1） B、（－1，0） C、（－1，－1） D、（0，－1）

查看试题解析
8. 如图，正比例函数 $y_{1} = k_{1} x (k_{1} < 0)$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} < 0)$ 的图象相交于A，B两点，点B的横坐标为2，当 $y_{1} > y_{2}$ 时，x的取值范围是（）

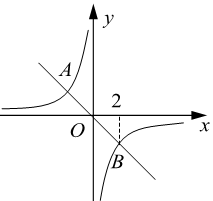A、 $x < - 2$ 或 $x > 2$ B、 $- 2 < x < 0$ 或 $x > 2$ C、 $x < - 2$ 或 $0 < x < 2$ D、 $- 2 < x < 0$ 或 $0 < x < 2$

查看试题解析
9. 已知一个直角三角形的两边长是方程 $x^{2} - 9 x + 20 = 0$ 的两个根，则这个直角三角形的斜边长为（）

A、3 B、 $\sqrt{41}$ C、3或 $\sqrt{41}$ D、5或 $\sqrt{41}$

查看试题解析
10. 已知抛物线y＝ax²＋bx＋c（a＞0），且a＋b＋c＝－1，a﹣b＋c＝－3．判断下列结论：①抛物线与x轴负半轴必有一个交点；②b＝1；③abc＞0； ④2a＋2b＋c＜0；⑤当0≤x≤2时，y_最大＝3a，其中正确结论的个数（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 将抛物线 $y = x^{2}$ 向下平移2个单位长度后，得到的抛物线解析式为．

查看试题解析
12. 已知关于x方程 $x^{2} - 3 x + m = 0$ 的一个根是1，则m的值等于．

查看试题解析
13. 反比例函数y＝ $\frac{m - 1}{x}$ 的图象在第一、三象限，则m的取值范围是．

查看试题解析
14. 在一个不透明袋子中，装有3个红球和一些白球，这些球除颜色外无其他差别，从袋中随机摸出一个球是红球的概率为 $\frac{1}{3}$ ，则袋中白球的个数是．

查看试题解析
15. 某种产品今年的年产量是20t，计划今后两年增加产量．如果每年的产量都比上一年增加x倍，两年后这种产品的产量y与x之间的函数表达式是．

查看试题解析
16. 如图，半径为2的扇形AOB的圆心角为120°，点C是弧AB的中点，点D、E是半径OA、OB上的动点，且满足∠DCE＝60°，则图中阴影部分面积等于．

查看试题解析
17. 如图，等腰Rt△ABC和等腰Rt△ADE的腰长分别为4和2，其中∠BAC＝∠DAE＝90°，点M为边DE的中点，若等腰Rt△ADE绕点A旋转，则点B到点M的距离最小值为．

查看试题解析

三、解答题

18. 解方程： $x^{2} - 1 = 4 x - 4$ ．

查看试题解析
19. 如图，M是CD的中点，EM⊥CD，若CD＝4，EM＝6，求 $\overset{⌢}{C E D}$ 所在圆的半径．

查看试题解析
20. 现有A、B两个不透明的袋子，A袋中的两个小球分别标记数字1，2；B袋中的三个小球分别标记数字3，4，5．这五个小球除标记的数字外，其余完全相同．分别将A、B两个袋子中的小球摇匀，然后小明从A、B袋中各随机摸出一个小球，请利用画树状图或列表的方法，求小明摸出的这两个小球标记的数字之和为5的概率．

查看试题解析
21. 在商场中，被称为“国货之星”某运动品牌的鞋子，每天可销售20双，每双可获利40元．为庆祝新年，对该鞋子进行促销活动，该鞋子每双每降价1元，平均每天可多售出2双．若设该鞋子每双降价x元，请解答下列问题：

(1)、用含x的代数式表示：降价x元后，每售出一双该鞋子获得利润是元，平均每天售出双该鞋子；

(2)、在此次促销活动中，每双鞋子降价多少元，可使该品牌的鞋子每天的盈利为1250元？

查看试题解析
22. 如图，正方形ABCD的边长为4，连接对角线AC，点E为BC边上一点，将线段AE绕点A逆时针旋转45°得到线段AF，点E的对应点F恰好落在边CD上，过F作FM⊥AC于点M．

(1)、求证：BE＝FM；

(2)、求BE的长度．

查看试题解析
23. 已知等边△OAB，边长为8，点A在y轴上，点B在第一象限，反比例函数 $y = \frac{k}{x}$ （x＞0）经过AB的中点M，与OB边相交于点N．

(1)、求k的值；

(2)、连接OM、MN，求△OMN的面积．

查看试题解析
24. 如图，△ABC内接于⊙O，AB为直径，点D为半径OA上一点，过点D作AB的垂线交AC于点E，交BC的延长线于点P，点F在线段PE上，且PF＝CF．

(1)、求证：CF是⊙O的切线；

(2)、连接AP与⊙O相交于点G，若∠ABC＝2∠PAC，求证：AB＝BP；

(3)、在（2）的条件下，若AC＝4，BC＝3，求CF的长．

查看试题解析
25. 抛物线y＝ax²＋bx－2（a≠0）与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C．

(1)、求抛物线的解析式；

(2)、如图1，抛物线的对称轴与x轴相交于点H，连接AC，BC．△ABC绕点B顺时针旋转一定角度后落在第一象限，当点C的对应点C₁落在抛物线的对称轴上时，求此时点A的对应点A₁的坐标；

(3)、如图2，过点C作 $C E ∥ x$ 轴交抛物线于点E，已知点D在抛物线上且横坐标为 $\frac{7}{2}$ ，在y轴左侧的抛物线上有一点P，满足∠PDC＝∠EDC，求点P的坐标．

查看试题解析