广东省清远市阳山县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 如图所示的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知反比例函数的图象经过点(﹣3,6),则k的值是( )A、﹣18 B、﹣2 C、2 D、183. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=34. 如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
2. 已知反比例函数的图象经过点(﹣3,6),则k的值是( )A、﹣18 B、﹣2 C、2 D、183. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=34. 如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )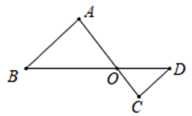 A、2 B、3 C、4 D、65. 如图,l1l2l3 , 直线a,b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB:AC=2:5,DE=6,则EF的长是( )
A、2 B、3 C、4 D、65. 如图,l1l2l3 , 直线a,b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB:AC=2:5,DE=6,则EF的长是( ) A、15 B、10 C、9 D、26. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数(x>0)的图象经过顶点B,则k的值为( )
A、15 B、10 C、9 D、26. 如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数(x>0)的图象经过顶点B,则k的值为( ) A、12 B、16 C、20 D、327. 同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )A、3.2米 B、4.8米 C、5.2米 D、5.6米8. 关于x的方程有两个不相等的实数根,则n的取值范围是( )A、n< B、n ≤ C、n> D、n>9. 在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 , 把△ABO缩小,则点A的对应点A′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)10. 下图中反比例函数 与一次函数 在同一直角坐标系中的大致图象是( )A、
A、12 B、16 C、20 D、327. 同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )A、3.2米 B、4.8米 C、5.2米 D、5.6米8. 关于x的方程有两个不相等的实数根,则n的取值范围是( )A、n< B、n ≤ C、n> D、n>9. 在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 , 把△ABO缩小,则点A的对应点A′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)10. 下图中反比例函数 与一次函数 在同一直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、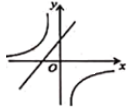
二、填空题
-
11. 若 , 则的值等于 .12. 若两个相似三角形的相似比是1:2,则它们的周长比是 .13. 在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外都相同.搅匀后从中任意摸出一个球,记下颜色再把它放回盒子中.不断重复实验多次后,摸到黑球的频率逐渐稳定在0.2左右.则据此估计盒子中大约有白球个.14. 已知关于x的一元二次方程的一个根是2,则k的值是 .15. 如图,已知ABC∽AMN,点M是AC的中点,AB=6,AC=8,则AN= .
 16. 2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价元,可列方程 .17. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .
16. 2021年端午节期间,合肥某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价元,可列方程 .17. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .三、解答题
-
18. 解方程: .19. 国庆期间,某电影院上映了《长津湖》《我和我父辈》《五个扑水的少年》三部电影.甲、乙两同学从中选取一部电影观看.求甲、乙两同学选取同一部电影的概率.20. 如图,在平行四边形ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且∠QPA=∠PCB.
求证:四边形ABCD是矩形.
 21. 如图,D、E、F分别是各边的中点,连接、、 .
21. 如图,D、E、F分别是各边的中点,连接、、 . (1)、求证:四边形为平行四边形;(2)、加上条件后,能使得四边形为菱形,请从①;②平分;③ , 这三个条件中选择条件填空(写序号),并加以证明.22. 2016 年,某市某楼盘以每平方米元的均价对外销售,因为楼 盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,年的均价为每平方米元(1)、求平均每年下调的百分率;(2)、假设年的均价仍然下调相同的百分率,张强准备购买一套平方米的住房, 他持有现金万元,可以在银行贷款万元,张强的愿望能否实现?为什么?(房价每平方米按照均价计算)23. 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
(1)、求证:四边形为平行四边形;(2)、加上条件后,能使得四边形为菱形,请从①;②平分;③ , 这三个条件中选择条件填空(写序号),并加以证明.22. 2016 年,某市某楼盘以每平方米元的均价对外销售,因为楼 盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,年的均价为每平方米元(1)、求平均每年下调的百分率;(2)、假设年的均价仍然下调相同的百分率,张强准备购买一套平方米的住房, 他持有现金万元,可以在银行贷款万元,张强的愿望能否实现?为什么?(房价每平方米按照均价计算)23. 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动. (1)、经过几秒△PCQ的面积为△ACB的面积的 ?(2)、经过几秒,△PCQ与△ACB相似?24. 已知C、D是双曲线上的两点,过点C作CA⊥x轴点A,过点D作DE⊥x轴点E,交OC于点F.
(1)、经过几秒△PCQ的面积为△ACB的面积的 ?(2)、经过几秒,△PCQ与△ACB相似?24. 已知C、D是双曲线上的两点,过点C作CA⊥x轴点A,过点D作DE⊥x轴点E,交OC于点F. (1)、如图1,若点D坐标为(1,1),OE:OA=1:3,则=(2)、如图2,延长OD,AC相交于点B,若点D为OB的中点.
(1)、如图1,若点D坐标为(1,1),OE:OA=1:3,则=(2)、如图2,延长OD,AC相交于点B,若点D为OB的中点.①当 , 求k的值;
②若点C的坐标是(6,1),试求四边形DFCB的面积.
25. 如图,在正方形中,点分别在边、上,与相交于点G,且 .(1)、如图1,求证:; (2)、如图2,与是方程的两个根,四边形的面积为 , 求正方形的面积.
(2)、如图2,与是方程的两个根,四边形的面积为 , 求正方形的面积. (3)、在第(2)题的条件下,如图3,延长BC至点N,使得CN=3,连接GN交CD于点M,直接写出线段的值.
(3)、在第(2)题的条件下,如图3,延长BC至点N,使得CN=3,连接GN交CD于点M,直接写出线段的值.