广东省广州市天河区2021-2022学年九年级上学期期末数学试题
试卷更新日期：2022-01-26 类型：期末考试
一、单选题
-
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（ ）A、
戴口罩讲卫生
B、
勤洗手勤通风
C、
有症状早就医
D、
少出门少聚集
2. 下列事件是必然事件的是（ ）A、同圆中，圆周角等于圆心角的一半 B、投掷一枚均匀的硬币100次，正面朝上的次数为50次 C、参加社会实践活动的367个同学中至少有两个同学的生日是同一天 D、把一粒种子种在花盆中，一定会发芽3. 抛物线y＝2（x+1）2不经过的象限是（ ）A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限4. 抛物线y＝（x+2）2+1可由抛物线y＝x2平移得到，下列平移正确的是（ ）A、先向右平移2个单位，再向上平移1个单位 B、先向右平移2个单位，再向下平移1个单位 C、先向左平移2个单位，再向上平移1个单位 D、先向左平移2个单位，再向下平移1个单位5. 在一只暗箱里放有a个除颜色外其他完全相同的球，这a个球中红球只有3个，每次将球搅拌均匀后，任意摸出1个球记下颜色再放回暗箱．通过大量重复摸球试验后发现，摸到红球的频率稳定在20%，那么可以推算a大约是（ ）A、15 B、12 C、9 D、46. 半径等于4的圆中，垂直平分半径的弦长为（ ）A、 B、 C、 D、7. 若x＝﹣1是关于x的一元二次方程ax2+bx﹣2＝0（a≠0）的一个根，则2021﹣2a+2b的值等于（ ）A、2015 B、2017 C、2019 D、20228. 如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画圆，则图中阴影部分图形的周长为（ ）
A、2π B、4π C、2π+12 D、4π+129. 在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法错误的是（ ）A、当a＜5时，点B在⊙A内 B、当1＜a＜5时，点B在⊙A内 C、当a＜1时，点B在⊙A外 D、当a＞5时，点B在⊙A外10. 如图，在Rt△ABC中，∠ACB＝90°，将Rt△ABC绕顶点C逆时针旋转得到Rt△A'B'C，M是BC的中点，P是A′B'的中点，连接PM．若BC＝2，∠BAC＝30°，则线段PM的最大值为（ ）．
A、2.5 B、2+ C、3 D、4二、填空题
-
11. 从一副没有“大小王”的扑克牌中随机地抽取一张，点数为“5”的概率是 ．12. 如图，在⊙O中，AC＝BD，若∠AOC＝120°，则∠BOD＝ ．
13. 已知圆锥的底面半径为7cm，它的侧面积是35πcm，则这个圆锥的母线长为 ．14. 已知二次函数y＝3（x﹣5）2 ， 当x分别取x1 ， x2（x1≠x2）时，函数值相等，则当x＝时，函数值为 ．15. 已知（x+3）（x﹣2）+m＝x2+x，则一元二次方程x2+x﹣m＝0的根是 ．16. 如图，将半径为4，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是 ．
三、解答题
-
17. 解方程：.18. 如图，在△ABC中，∠CAB＝70°，在同一平面内，将△ABC绕点A旋转到△AB'C′的位置，使得CC′AB，求∠CC'A的度数．
19. 在“双减”政策下，某学校自主开设了A书法、B篮球、C足球、D器乐四门选修课程供学生选择，每门课程被选到的机会均等．若小明和小刚两位同学各计划选修一门课程，请用列表或树状图求他们两人恰好同时选修球类的概率．20. 如图，在△ABC中，∠A＝∠B＝30°．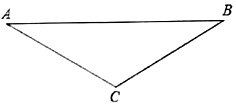
(1)、尺规作图：在线段AB上找一点O，以O为圆心作圆，使⊙O经过B，C两点．(2)、求证：AC与（1）中所做的⊙O相切．21. 在△ABC中，AB＝BC＝4，∠ABC＝90°，M是AC的中点，点N在边AB上（不与点A，B重合），将△ANM绕点M逆时针旋转90°得到△BPM．问：△BPN的面积能否等于3，请说明理由．
22. 如图，PA，PB与⊙O相切，切点为A，B，CD与⊙O相切于点E，分别交PA，PB于点D，C．若PA，PB的长是关于x的一元二次方程x2﹣mx+m﹣1＝0的两个根．
(1)、求m的值；(2)、求△PCD的周长．23. 某企业投资100万元引进一条农产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万元，但使用8年后生产线报废该，生产线投产后，从第1年到第x年的维修、保养费用累计为y万元，且y＝ax2+bx，若第1年的维修、保养费为2万元，第2年的为4万元．(1)、求a的值；(2)、小敏同学依题意判断，这条生产线在第四年能收回投资款，并在报废前能盈利100万元．你认为这个判断符合题意吗？请说明理由．24. 已知，P是直线AB上一动点（不与A，B重合），以P为直角顶点作等腰直角三角形PBD，点E是直线AD与△PBD的外接圆除点D以外的另一个交点，直线BE与直线PD相交于点F．(1)、如图，当点P在线段AB上运动时，若∠DBE＝30°，PB＝2，求DE的长；(2)、当点P在射线AB上运动时，试探求线段AB，PB，PF之间的数量关系，并给出证明．25. 已知二次函数y＝﹣9x2﹣6ax﹣a2+2a．(1)、当a＝1时，求该二次函数的最大值；(2)、若该二次函数图象与坐标轴有两个交点，求实数a的值；(3)、若该二次函数在﹣≤x≤有最大值﹣3，求实数a的值．