北京市通州区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-26 类型:期末考试
一、单选题
-
1. 已知二次函数的图象如图所示,关于a,c的符号判断正确的是( )
 A、a>0,c>0 B、a>0,c<0 C、a<0,c>0 D、a<0,c<02. 如图, 的顶点位于正方形网格的格点上,若 ,则满足条件的 是( )A、
A、a>0,c>0 B、a>0,c<0 C、a<0,c>0 D、a<0,c<02. 如图, 的顶点位于正方形网格的格点上,若 ,则满足条件的 是( )A、 B、
B、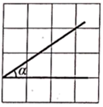 C、
C、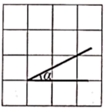 D、
D、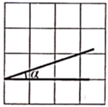 3. 在半径为6cm的圆中,的圆心角所对弧的弧长是( )A、cm B、cm C、cm D、cm4. 如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( )
3. 在半径为6cm的圆中,的圆心角所对弧的弧长是( )A、cm B、cm C、cm D、cm4. 如图,点A,B,C均在⊙O上,连接OA,OB,AC,BC,如果OA⊥OB,那么∠C的度数为( ) A、22.5° B、45° C、90° D、67.5°5. 如图,在 中,E为BC的中点,DE、AC交于点F,则 的值为( )
A、22.5° B、45° C、90° D、67.5°5. 如图,在 中,E为BC的中点,DE、AC交于点F,则 的值为( ) A、1 B、 C、 D、6. 如图,是的直径,点D在的延长线上,切于点C.若 , , 则等于( ).
A、1 B、 C、 D、6. 如图,是的直径,点D在的延长线上,切于点C.若 , , 则等于( ). A、6 B、4 C、 D、37. 如图,某停车场入口的栏杆从水平位置绕点O旋转到的位置.已知米,若栏杆的旋转角 , 则栏杆端点A上升的垂直距离为( )
A、6 B、4 C、 D、37. 如图,某停车场入口的栏杆从水平位置绕点O旋转到的位置.已知米,若栏杆的旋转角 , 则栏杆端点A上升的垂直距离为( ) A、米 B、米 C、米 D、米8. 某同学将如图所示的三条水平直线 , , 的其中一条记为x轴(向右为正方向),三条竖直直线 , , 的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数的图象,那么她所选择的x轴和y轴分别为直线( )
A、米 B、米 C、米 D、米8. 某同学将如图所示的三条水平直线 , , 的其中一条记为x轴(向右为正方向),三条竖直直线 , , 的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数的图象,那么她所选择的x轴和y轴分别为直线( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题
-
9. 如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪,从量角器的点A处观测,当量角器的0刻度线对准旗杆顶端时,铅垂线对应的度数是 , 则此时观测旗杆顶端的仰角度数是 .
 10. 如图,在ABC中,∠C=90°,AB=10,在同一平面内,点O到点A,B,C的距离均等于a(a为常数).那么常数a的值等于 .
10. 如图,在ABC中,∠C=90°,AB=10,在同一平面内,点O到点A,B,C的距离均等于a(a为常数).那么常数a的值等于 . 11. 在ABC中, , , , 那么的长为 .12. 已知P( , 1),Q( , 1)两点都在抛物线上,那么 .13. 如图,在测量旗杆高度的数学活动中,某同学在地面放了一个平面镜C,然后向后退,直到他刚好在镜子中看到旗杆的顶部A.如果他的眼睛到地面的距离ED=1.6m,同时量得他到平面镜C的距离DC=2m,平面镜C到旗杆的底部B的距离CB=15m,那么旗杆高度AB=m.
11. 在ABC中, , , , 那么的长为 .12. 已知P( , 1),Q( , 1)两点都在抛物线上,那么 .13. 如图,在测量旗杆高度的数学活动中,某同学在地面放了一个平面镜C,然后向后退,直到他刚好在镜子中看到旗杆的顶部A.如果他的眼睛到地面的距离ED=1.6m,同时量得他到平面镜C的距离DC=2m,平面镜C到旗杆的底部B的距离CB=15m,那么旗杆高度AB=m. 14. 如图,过点A(0,4)作平行于x轴的直线AC分别交抛物线与于B、C两点,那么线段BC的长是 .
14. 如图,过点A(0,4)作平行于x轴的直线AC分别交抛物线与于B、C两点,那么线段BC的长是 . 15. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为m.
15. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,则筒车工作时,盛水桶在水面以下的最大深度为m. 16. 如图,ABC的两条中线BE,CD交于点M.某同学得出以下结论:①;②ADE∽ABC;③;④ . 其中结论正确的是:(只填序号).
16. 如图,ABC的两条中线BE,CD交于点M.某同学得出以下结论:①;②ADE∽ABC;③;④ . 其中结论正确的是:(只填序号).
三、解答题
-
17. 在平面直角坐标系xOy中,二次函数的图象经过点 . 求此二次函数的表达式及顶点的坐标.18. 如图,在 中, , , .求 , 和 .
 19. 如图, , 点B、C分别在AM、AN上,且 .
19. 如图, , 点B、C分别在AM、AN上,且 . (1)、尺规作图:作∠CBM的角平分线BD,BD与AN相交于点D;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求证:ABC∽ADB.20. 已知关于x的二次函数 .
(1)、尺规作图:作∠CBM的角平分线BD,BD与AN相交于点D;(保留作图痕迹,不写作法)(2)、在(1)所作的图中,求证:ABC∽ADB.20. 已知关于x的二次函数 . (1)、如果二次函数的图象与x轴交于A,B两点(点A在点B的左侧),且AB=2,求m的值;(2)、若对于每一个x值,它所对应的函数值都不小于1,求m的取值范围.21. 已知:A,B是直线l上的两点.
(1)、如果二次函数的图象与x轴交于A,B两点(点A在点B的左侧),且AB=2,求m的值;(2)、若对于每一个x值,它所对应的函数值都不小于1,求m的取值范围.21. 已知:A,B是直线l上的两点.求作:ABC,使得点C在直线l上方,且AC=BC, .

作法:①分别以A,B为圆心,AB长为半径画弧,在直线l上方交于点O,在直线l下方交于点E;
②以点O为圆心,OA长为半径画圆;
③作直线OE与直线l上方的⊙O交于点C;
④连接AC,BC.ABC就是所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接OA,OB.
∵OA=OB=AB,
∴OAB是等边三角形.
∴ .
∵A,B,C在⊙O上,
∴∠ACB=∠AOB( )(填推理的依据).
∴ .
由作图可知直线OE是线段AB的垂直平分线,
∴AC=BC( )(填推理的依据).
∴ABC就是所求作的三角形.
22. 如图,在⊙O中,点E是弦CD的中点,过点O,E作直径AB(AE>BE),连接BD,过点C作CFBD交AB于点G,交⊙O于点F,连接AF.求证:AG=AF.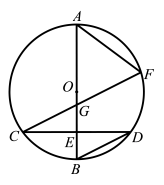 23. 已知一个二次函数的表达式为 .
23. 已知一个二次函数的表达式为 . (1)、当时,若P( , ),Q(m,b)两点在该二次函数图象上,求m的值;(2)、已知点A( , 0),B( , ),二次函数的图象与线段AB只有一个公共点,直接写出a的取值范围.24. 如图,ABC是⊙O的内接三角形, , , 连接AO并延长交⊙O于点D,过点C作⊙O的切线,与BA的延长线相交于点E.
(1)、当时,若P( , ),Q(m,b)两点在该二次函数图象上,求m的值;(2)、已知点A( , 0),B( , ),二次函数的图象与线段AB只有一个公共点,直接写出a的取值范围.24. 如图,ABC是⊙O的内接三角形, , , 连接AO并延长交⊙O于点D,过点C作⊙O的切线,与BA的延长线相交于点E. (1)、求证:AD∥EC;(2)、若AD=6,求线段AE的长.25. 二次函数的图象与y轴交于点A,将点A向右平移4个单位长度,得到点B,点B在二次函数的图象上.
(1)、求证:AD∥EC;(2)、若AD=6,求线段AE的长.25. 二次函数的图象与y轴交于点A,将点A向右平移4个单位长度,得到点B,点B在二次函数的图象上. (1)、求点B的坐标(用含a的代数式表示);(2)、二次函数的对称轴是直线;(3)、已知点( , ),( , ),( , )在二次函数的图象上.若 , 比较 , , 的大小,并说明理由.26. 如图,O为四边形ABCD内一点,E为AB的中点,OA=OD,OB=OC,∠AOB+∠COD= .
(1)、求点B的坐标(用含a的代数式表示);(2)、二次函数的对称轴是直线;(3)、已知点( , ),( , ),( , )在二次函数的图象上.若 , 比较 , , 的大小,并说明理由.26. 如图,O为四边形ABCD内一点,E为AB的中点,OA=OD,OB=OC,∠AOB+∠COD= .
 (1)、若∠BOE=∠BAO,AB= , 求OB的长;(2)、用等式表示线段OE和CD之间的关系,并证明.27. 在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的“近距离”,记为d(M,N),特别地,若图形M,N有公共点,规定d(M,N)=0.已知:如图,点A( , 0),B(0,).
(1)、若∠BOE=∠BAO,AB= , 求OB的长;(2)、用等式表示线段OE和CD之间的关系,并证明.27. 在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的“近距离”,记为d(M,N),特别地,若图形M,N有公共点,规定d(M,N)=0.已知:如图,点A( , 0),B(0,).
 (1)、如果⊙O的半径为2,那么d(A,⊙O)= , d(B,⊙O)= .(2)、如果⊙O的半径为r,且d(⊙O,线段AB)=0,求r的取值范围;(3)、如果C(m,0)是x轴上的动点,⊙C的半径为1,使d(⊙C,线段AB)<1,直接写出m的取值范围.
(1)、如果⊙O的半径为2,那么d(A,⊙O)= , d(B,⊙O)= .(2)、如果⊙O的半径为r,且d(⊙O,线段AB)=0,求r的取值范围;(3)、如果C(m,0)是x轴上的动点,⊙C的半径为1,使d(⊙C,线段AB)<1,直接写出m的取值范围.