北京市石景山区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $2 y = 5 x (x y \neq 0)$ ，则下列比例式正确的是（）

A、 $\frac{x}{y} = \frac{5}{2}$ B、 $\frac{x}{5} = \frac{2}{y}$ C、 $\frac{x}{y} = \frac{2}{5}$ D、 $\frac{y}{x} = \frac{2}{5}$

查看试题解析
2. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ．若 $A C = 4$ ， $B C = 3$ ，则 $s i n A$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{4}{5}$

查看试题解析
3. 在平面直角坐标系xOy中，抛物线 $y = x^{2}$ 向上平移2个单位长度得到的抛物线为（）

A、 $y = {(x + 2)}^{2}$ B、 $y = {(x - 2)}^{2}$ C、 $y = x^{2} - 2$ D、 $y = x^{2} + 2$

查看试题解析
4. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的示意图如图所示，下列说法中正确的是（）

A、 $a < 0$ B、 $b < 0$ C、 $c > 0$ D、 $Δ > 0$

查看试题解析
5. 在平面直角坐标系xOy中，若函数 $y = \frac{k}{x} (x < 0)$ 的函数值y随着自变量x的增大而增大，则函数 $y = \frac{k}{x} (x < 0)$ 的图象所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，四边形ABCD内接于 $⊙ O$ ，若四边形ABCO是菱形，则 $∠ D$ 的度数为（）

A、45° B、60° C、90° D、120°

查看试题解析
7. 正方形的面积y与它的周长x满足的函数关系是（）

A、正比例函数 B、一次函数 C、二次函数 D、反比例函数

查看试题解析
8. 在平面直角坐标系xQy中，点 $(- 1 ， y_{1})$ ， $(2 ， y_{2})$ ， $(4 ， y_{3})$ 在抛物线 $y = a x^{2} - 2 a x + c$ 上．当 $a > 0$ 时，下列说法一定正确的是（）

A、若 $y_{1} y_{2} < 0$ ，则 $y_{3} > 0$ B、若 $y_{2} y_{3} > 0$ ，则 $y_{1} < 0$ C、若 $y_{1} y_{3} < 0$ ，则 $y_{2} > 0$ D、若 $y_{1} y_{2} y_{3} = 0$ ，则 $y_{2} = 0$

查看试题解析

二、填空题

9. 如图， $A B ∥ C D$ ， AD，BC交于点O， $\frac{A O}{O D} = \frac{1}{2}$ ．若 $B O = 3$ ，则OC的长为．

查看试题解析
10. 在半径为3的圆中，60°的圆心角所对的劣弧长等于．

查看试题解析
11. 如图，在平面直角坐标系xOy中，P为函数 $y = \frac{m}{x} (x > 0)$ 图象上一点，过点P分别作x轴、y轴的垂线，垂足分别为M，N．若矩形PMON的面积为3，则m的值为．

查看试题解析
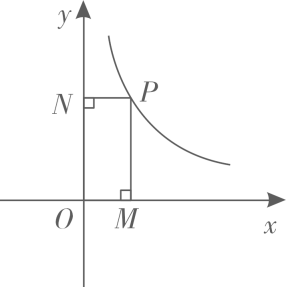12. 如图， $△ A B C$ 的高AD，BE相交于点O，写出一个与 $△ A O E$ 相似的三角形，这个三角形可以是．

查看试题解析
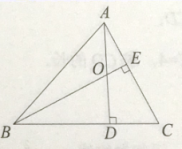13. 如图，PA，PB是 $⊙ O$ 的切线，切点分别为A，B．若 $∠ O A B = 30 °$ ， $P A = 3$ ，则AB的长为．

查看试题解析
14. 有一块三角形的草坪，其中一边的长为10m．在这块草坪的图纸上，这条边的长为5cm．已知图纸上的三角形的周长为15cm，则这块草坪的周长为m．

查看试题解析
15. 北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素．如图，赛道剖面图的一部分可抽象为线段AB．已知坡AB的长为30m，坡角 $∠ A B H$ 约为37°，则坡AB的铅直高度AH约为m．（参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ．）

查看试题解析
16. 如图，在平面直角坐标系xOy中，P为x轴正半轴上一点．已知点 $A (0 ， 2)$ ， $B (0 ， 8)$ ， $⊙ M$ 为 $△ A B P$ 的外接圆．

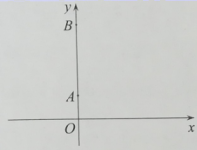(1)、点M的纵坐标为；

(2)、当 $∠ A P B$ 最大时，点P的坐标为．

查看试题解析

三、解答题

17. 计算： $\sqrt{3} t a n 60 ° - 4 c o s 45 ° - {(π - 1)}^{0} + \sqrt{8}$ ．

查看试题解析
18. 如图，AE平分 $∠ B A C$ ， D为AE上一点， $∠ B = ∠ C$ ．

(1)、求证： $△ A B E ∼ △ A C D$ ；

(2)、若D为AE中点， $B E = 4$ ，求CD的长．

查看试题解析
19. 在平面直角坐标系xOy中，已知抛物线 $y = x^{2} - 4 x + 3$ ．

(1)、求它的顶点坐标；

(2)、求它与x轴的交点坐标．

查看试题解析
20. 下面是小石设计的“过三角形一个顶点作其对边的平行线”的尺规作图过程．
已知：如图， $△ A B C$ ．
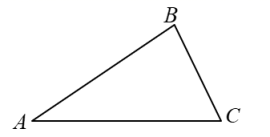
求作：直线BD，使得 $B D ∥ A C$ ．
作法：如图，
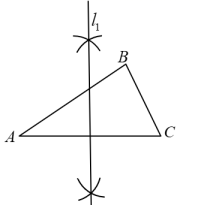
①分别作线段AC，BC的垂直平分线 $l_{1}$ ， $l_{2}$ ，两直线交于点O；
②以点O为圆心，OA长为半径作圆；
③以点A为圆心，BC长为半径作孤，交 $\overset{⌢}{A B}$ 于点D；
④作直线BD．所以直线BD就是所求作的直线．
根据小石设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；（保留作图痕迹）

(2)、完成下面的证明．
证明：连接AD，
∵点A，B，C，D在 $⊙ O$ 上， $A D = B C$ ，
∴ $\overset{⌢}{A D} =$ ▲ ．
∴ $∠ D B A = ∠ C A B$ （）（填推理的依据）．
∴ $B D ∥ A C$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B = 45 °$ ， $t a n C = \frac{2}{3}$ ， $A C = 2 \sqrt{13}$ ，求BC的长．

查看试题解析
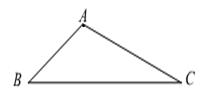22. 在平面直角坐标系xOy中，二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
x
…
－1
0
1
2
…
y
…
－3
0
1
0
…

(1)、求这个二次函数的表达式；

(2)、画出这个二次函数的图象；

(3)、若 $y < - 3$ ，结合函数图象，直接写出x的取值范围．

查看试题解析
23. 如图，AB为 $⊙ O$ 的直径，点C在 $⊙ O$ 上，连接AC，BC，过点O作 $O D ⊥ B C$ 于点D，过点C作 $⊙ O$ 的切线交OD的延长线于点E．

(1)、求证： $∠ E = ∠ B$ ；

(2)、连接AD．若 $C E = 4 \sqrt{5}$ ， $B C = 8$ ，求AD的长．

查看试题解析
24. 如图，排球运动场的场地长18m，球网高度2.24m，球网在场地中央，距离球场左、右边界均为9m．一名球员在场地左侧边界练习发球，排球的飞行路线可以看作是对称轴垂直于水平面的抛物线的一部分．某次发球，排球从左边界的正上方发出，击球点的高度为2m，当排球飞行到距离球网3m时达到最大高度2.5m．小石建立了平面直角坐标系xOy（1个单位长度表示1m），求得该抛物线的表达式为 $y = - \frac{1}{72} x^{2} + \frac{5}{2}$ ．根据以上信息，回答下列问题：

(1)、画出小石建立的平面直角坐标系；

(2)、判断排球能否过球网，并说明理由．

查看试题解析
25. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象过点 $A (2 ， 3)$ ．

(1)、求k的值；

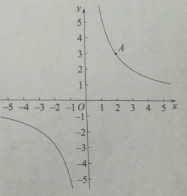(2)、过点 $P (m ， 0) (m \neq 0)$ 作x轴的垂线，分别交反比例函数 $y = \frac{k}{x} (k \neq 0)$ ， $y = - \frac{4}{x}$ 的图象于点M，N．
①当 $m = - 2$ 时，求MN的长；
②若 $M N \geq 5$ ，直接写出m的取值范围．

查看试题解析
26. 在平面直角坐标系xOy中， $A (m - 1 ， y_{1})$ ， $B (3 ， y_{2})$ 是抛物线 $y = x^{2} - 2 m x + m^{2} - 4$ 上两点．

(1)、将 $y = x^{2} - 2 m x + m^{2} - 4$ 写成 $y = a {(x - h)}^{2} + k$ 的形式；

(2)、若 $m = 0$ ，比较 $y_{1}$ ， $y_{2}$ 的大小，并说明理由；

(3)、若 $y_{1} < y_{2}$ ，直接写出m的取值范围．

查看试题解析
27. 如图，AD是 $△ A B C$ 的高，点B关于直线AC的对称点为E，连接CE，F为线段CE上—点（不与点E重合）， $A F = A B$ ．

(1)、比较 $∠ A F E$ 与 $∠ A B C$ 的大小；

(2)、用等式表示线段BD，EF的数量关系，并证明；

查看试题解析
28. 在平面直角坐标系xOy中， $⊙ O$ 的半径为2．点P，Q为 $⊙ O$ 外两点，给出如下定义：若 $⊙ O$ 上存在点M，N，使得P，Q，M，N为顶点的四边形为矩形，则称点P，Q是 $⊙ O$ 的“成对关联点”．

(1)、如图，点A，B，C，D横、纵坐标都是整数．在点B，C，D中，与点A组成 $⊙ O$ 的“成对关联点”的点是；

(2)、点 $E (t ， t)$ 在第一象限，点F与点E关于x轴对称．若点E，F是 $⊙ O$ 的“成对关联点”，直接写出t的取值范围；

(3)、点G在y轴上．若直线 $y = 4$ 上存在点H，使得点G，H是 $⊙ O$ 的“成对关联点”，直接写出点G的纵坐标 $y_{G}$ 的取值范围．

查看试题解析

x	…	－1	0	1	2	…
y	…	－3	0	1	0	…