北京市平谷区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 如果3x=5y，则下列比例式成立的是（　　）

A、 $\frac{x}{y} = \frac{3}{5}$ B、 $\frac{x}{y} = \frac{5}{3}$ C、 $\frac{x}{3} = \frac{y}{5}$ D、 $\frac{3}{x} = \frac{5}{y}$

查看试题解析
2. 如图，在△ABC中，DE//BC， $\frac{A D}{B D}$ =2，若AE=6，则EC的值为（）

A、3 B、2 C、1 D、9

查看试题解析
3. 将抛物线 $y = 2 x^{2}$ 向右平移2个单位，再向上平移3个单位得到的抛物线是（）

A、 $y = 2 {(x - 2)}^{2} + 3$ B、 $y = 2 {(x - 2)}^{2} - 3$ C、 $y = 2 {(x + 2)}^{2} - 3$ D、 $y = 2 {(x + 2)}^{2} + 3$

查看试题解析
4. 如图，角 $α$ 在边长为1的正方形网格中，则 $t a n α$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3 \sqrt{13}}{13}$ C、 $\frac{2 \sqrt{13}}{13}$ D、 $\frac{3}{2}$

查看试题解析
5. 如图，AB 为⊙O 的直径，弦 CDAB，垂足为点 E，若 ⊙O的半径为5，CD=8，则AE的长为（）

A、3 B、2 C、1 D、 $\sqrt{3}$

查看试题解析
6. 如图，Rt△ABC中，∠ACB=90°，∠B=30°，作∠CAD=30°，CD⊥AD于D，若△ADC的面积为1，则△ABC的面积为（）

A、2 B、3 C、4 D、8

查看试题解析
7. 为了解不等式“ $\frac{1}{m} < m$ ”，明明绘制了如图所示的函数图象，通过观察图象，该不等式的解集为（）

A、 $m > 1$ B、 $m < - 1$ C、 $m < - 1$ 或 $0 < m < 1$ D、 $m > 1$ 或 $- 1 < m < 0$

查看试题解析
8. 用长为2米的绳子围成一个矩形，它的一边长为x米，设它的面积为S平方米，则S与x的函数关系为（）

A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系

查看试题解析

二、填空题

9. 函数y= $\frac{1}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
10. 如图，在⊙O中，A，B，C是⊙O上三点，如果∠AOB=70°，那么∠C的度数为．

查看试题解析
11. 如图，若点P在反比例函数y＝﹣ $\frac{3}{x}$ （x＜0）的图象上，过点P作PM⊥x轴于点M，PN⊥y轴于点N，则矩形PMON的面积为.

查看试题解析
12. 在Rt△ABC中，∠C=90°，如果cosA= $\frac{1}{3}$ ， AC=2，那么AB的长为．

查看试题解析
13. 如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为2m，旗杆底部与平面镜的水平距离为12m．若小明的眼睛与地面的距离为1.5m，则旗杆的高度为．（单位：m）

查看试题解析
14. 二次函数 $y = x^{2} - 2 x + k$ 的图象与x轴有两个交点，则k的取值范围是．

查看试题解析
15. 如图， $P A ， P B$ 是 $⊙ O$ 的切线， $A ， B$ 是切点．若 $∠ P = 50 °$ ，则 $∠ A O B =$ ．

查看试题解析
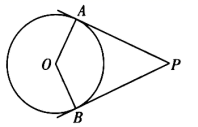16. 某地的药材批发公司指导农民养植和销售某种药材，经市场调研发现1-8月份这种药材售价（元）与月份之间存在如下表所示的一次函数关系，同时，每千克的成本价（元）与月份之间近似满足如图所示的抛物线，观察两幅图表，试判断月份出售这种药材获利最大．
月份
...
3
6
...
每千克售价
...
8
6
...

查看试题解析

三、解答题

17. 计算： $| - \sqrt{3} | + {(\frac{1}{2})}^{- 1} - \sqrt{12} + 2 c o s 30 °$ ．

查看试题解析
18. 如图，在△ABC中，点D在AB边上，∠ABC=∠ACD，

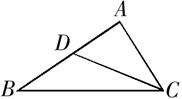(1)、求证：△ABC∽△ACD

(2)、若AD=2，AB=5.求AC的长．

查看试题解析
19. 已知二次函数 $y = x^{2} + 2 x - 3$ ．

(1)、求该二次函数图象的顶点坐标；

(2)、求该二次函数图象与x轴、y轴的交点；

(3)、在平面直角坐标系xOy中，画出二次函数 $y = x^{2} + 2 x - 3$ 的图象；

(4)、结合函数图象，直接写出当 $y < 0$ 时，x的取值范围．

查看试题解析
20. 如图，A是 $⊙ O$ 上一点，过点A作 $⊙ O$ 的切线．

(1)、①连接OA并延长，使AB=OA；
②作线段OB的垂直平分线；使用直尺和圆规，在图中作OB的垂直平分线l（保留作图痕迹）．

(2)、直线l即为所求作的切线，完成如下证明．
证明：在 $⊙ O$ 中，∵直线l垂直平分OB
∴直线l经过半径OA的外端，且，
∴直线l是 $⊙ O$ 的切线（）（填推理的依据）．

查看试题解析
21. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象过点A（0，3），B（2，3），C（-1，0）则

(1)、该抛物线的对称轴为；

(2)、该抛物线与x轴的另一个交点为；

(3)、求该抛物线的表达式．

查看试题解析
22. 因为一条湖的阻断，无法测量AC两地之间的距离，在湖的一侧取点B，使得点A恰好位于点B北偏东70°方向处，点C恰好位于点B的西北方向上，若经过测量，AB=10千米．你能否经过计算得出AC之间的距离．（精确到0.1，参考数据：sin70°≈0.94，cos70°≈0.34）

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $y = \frac{1}{2} x + 1$ 交于点 $A (2 ， a)$ ．

(1)、求a、k的值；

(2)、已知点 $P (n ， 0) (n > 0)$ ，过点P作垂直于x轴的直线，与反比例函数图象交于点B，与直线交于点C．横、纵坐标都是整数的点叫做整点．记反比例函数图象在点A，B之间的部分与线段 $A C$ ， $B C$ 围成的区域（不含边界）为Ｗ．
①当 $n = 5$ 时，直接写出区域Ｗ内的整点个数；
②若区域Ｗ内的整点恰好为2个，结合函数图象，直接写出n的取值范围．

查看试题解析
24. 如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，半径OD $∥$ 弦BC．

(1)、求证：弧AD=弧CD；

(2)、连接AC、BD相交于点F，AC与OD相交于点E，连接CD，若⊙O的半径为5，BC=6，求CD和EF的长．

查看试题解析
25. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，过点C作CE∥AB，过点A作AE∥CD，两线相交于点E，连接DE．

(1)、求证：四边形AECD是矩形；

(2)、若 $B D = 4 \sqrt{5} ， s i n ∠ A C E = \frac{2 \sqrt{5}}{5}$ ，求DE的长．

查看试题解析
26. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} + b x + a - 2 (a > 0)$ 的对称轴是直线x＝1．

(1)、用含a的式子表示b；

(2)、若当－2≤x≤3时，y的最大值是7，求a的值；

(3)、若点A（-2，m），B（3，n）为抛物线上两点，且mn<0，求a的取值范围．

查看试题解析
27. 如图，∠MAN=45°，B是射线AN上一点，过B作BC⊥AM于点C，点D是BC上一点，作射线AD，过B作BE⊥AD于点E，连接CE．

(1)、依题意补全图形；

(2)、求证：∠CAE=∠DBE；

(3)、用等式表示线段CE、BE、AE的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，点A（0，-1），以O为圆心，OA长为半径画圆，P为平面上一点，若存在⊙O上一点B，使得点P关于直线AB的对称点在⊙O上，则称点P是⊙O的以A为中心的“关联点”．

(1)、如图，点 $P_{1} (- 1 ， 0)$ ， $P_{2} (\frac{1}{2} ， \frac{1}{2})$ ， $P_{3} (0 ， \frac{6}{5})$ 中，⊙O的以点A为中心的“关联点”是；

(2)、已知点P（m，0）为x轴上一点，若点P是⊙O的以A为中心的“关联点”，直接写出m的取值范围；

(3)、C为坐标轴上一点，以OC为一边作等边△OCD，若CD边上至少有一个点是⊙O的以点A为中心的“关联点”，求CD长的最大值．

查看试题解析

月份	...	3	6	...
每千克售价	...	8	6	...