北京市大兴区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称图形也是轴对称图形的是（）

A、圆 B、平行四边形 C、直角三角形 D、等边三角形

查看试题解析
2. 抛物线 $y = {(x + 1)}^{2} + 2$ 的顶点坐标是（）

A、（1，2） B、（1， $- 2$ ） C、（ $- 1$ ， 2） D、（ $- 1$ ， $- 2$ ）

查看试题解析
3. 以下事件为随机事件的是（）

A、通常加热到100℃时，水沸腾 B、篮球队员在罚球线上投篮一次，未投中 C、任意画一个三角形，其内角和是360° D、半径为2的圆的周长是 $4 π$

查看试题解析
4. 如图， $△ A B C$ 中， $∠ A B C = 50 °$ ， $∠ A C B = 74 °$ ，点O是 $△ A B C$ 的内心．则 $∠ B O C$ 等于（）

A、124° B、118° C、112° D、62°

查看试题解析
5. 下列所给方程中，没有实数根的是（）

A、 $x^{2} + 2 x = 0$ B、 $5 x^{2} - 4 x - 2 = 0$ C、 $3 x^{2} - 4 x + 1 = 0$ D、 $4 x^{2} - 3 x + 2 = 0$

查看试题解析
6. 将二次函数 $y = x^{2} - 4 x + 5$ 用配方法化为 $y = {(x - h)}^{2} + k$ 的形式，结果为（）

A、 $y = {(x - 4)}^{2} + 1$ B、 $y = {(x - 4)}^{2} - 1$ C、 $y = {(x - 2)}^{2} - 1$ D、 $y = {(x - 2)}^{2} + 1$

查看试题解析
7. 如图， $⊙ C$ 与 $∠ A O B$ 的两边分别相切，其中OA边与 $⊙ C$ 相切于点P．若 $∠ A O B = 90 °$ ， $O P = 4$ ，则OC的长为（）

A、8 B、 $16 \sqrt{2}$ C、 $4 \sqrt{2}$ D、 $2 \sqrt{2}$

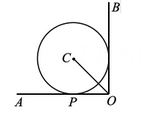查看试题解析
8. 小亮、小明、小刚三名同学中，小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，并且小亮与小刚的年龄的乘积是130.你知道这三名同学的年龄各是多少岁吗？设小明的年龄为x岁，则可列方程为（）

A、 $(x + 2) (x - 1) = 130$ B、 $(x - 2) (x + 1) = 130$ C、 $x (x - 2) = 130$ D、 $x (x + 1) = 130$

查看试题解析

二、填空题

9. 一元二次方程 $x^{2} - 3 x = 0$ 的根是．

查看试题解析
10. 如图，A、B、C是⊙O上的点，若∠AOB=70°，则∠ACB的度数为．

查看试题解析
11. 已知抛物线 $y = x^{2} - x - 3$ 经过点 $A (2 ， y_{1})$ 、 $B (3 ， y_{2})$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是．

查看试题解析
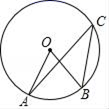12. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB＝15°，则∠AOB′的度数是．

查看试题解析
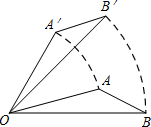13. 圆心角是270°的扇形的半径为4cm，则这个扇形的面积是 $c m^{2}$ ．

查看试题解析
14. 请写出一个开口向上，并且对称轴为直线x=1的抛物线的表达式y= ．

查看试题解析
15. 若一个扇形的半径是18cm，且它的弧长是 $6 π c m$ ，则此扇形的圆心角等于．

查看试题解析
16. 已知点A的坐标为 $(a ， b)$ ， O为坐标原点，连结OA，将线段OA绕点О顺时针旋转90°得到线段 $O A_{1}$ ，则点 $A_{1}$ 的坐标为．

查看试题解析

三、解答题

17. 计算： $\sqrt{27} + {(3 - π)}^{0} + | 1 - \sqrt{3} | + 3 \times \frac{1}{\sqrt{3}}$ ．

查看试题解析
18. 在平面直角坐标系 $x O y$ 中，二次函数 $y = x^{2} - 2 m x + 5 m$ 的图象经过点 $(1 ， - 2)$ ．

(1)、求二次函数的表达式；

(2)、求二次函数图象的对称轴．

查看试题解析

19. 同时掷两枚质地均匀的骰子，两枚骰子分别记为第1枚和第2枚，下表列举出了所有可能出现的结果．

第2枚第1枚	1	2	3	4	5	6
1	（1，1）	（2，1）	（3，1）	（4，1）	（5，1）	（6，1）
2	（1，2）	（2，2）	（3，2）	（4，2）	（5，2）	（6，2）
3	（1，3）	（2，3）	（3，3）	（4，3）	（5，3）	（6，3）
4	（1，4）	（2，4）	（3，4）	（4，4）	（5，4）	（6，4）
5	（1，5）	（2，5）	（3，5）	（4，5）	（5，5）	（6，5）
6	（1，6）	（2，6）	（3，6）	（4，6）	（5，6）	（6，6）

(1)、由上表可以看出，同时掷两枚骰子，可能出现的结果有36种，并且它们出现的可能性（填“相等”或者“不相等”）；

(2)、计算下列事件的概率：

①两枚骰子的点数相同；

②至少有一枚骰子的点数为3.

查看试题解析

20. 下面是“作一个角的平分线”的尺规作图过程．
已知：如图，钝角 $∠ A O B$ ．
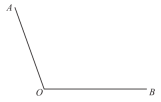
求作：射线OC，使 $∠ A O C = ∠ B O C$ ．
作法：如图，
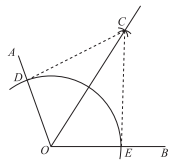
①在射线OA上任取一点D；
②以点О为圆心，OD长为半径作弧，交OB于点E；
③分别以点D，E为圆心，大于 $\frac{1}{2} D E$ 长为半径作弧，在 $∠ A O B$ 内，两弧相交于点C；
④作射线OC．
则OC为所求作的射线．
完成下面的证明．
证明：连接CD，CE
由作图步骤②可知 $O D =$       ▲ ．
由作图步骤③可知 $C D =$             ▲                   ．
∵ $O C = O C$ ，
∴ $△ O C D ≌ △ O C E$ ．
∴ $∠ A O C = ∠ B O C$ （      ）（填推理的依据）．

查看试题解析
21. 如图，AB是⊙O 的直径，CD是⊙O的一条弦，且CD⊥AB 于点E．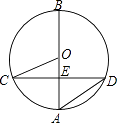

(1)、求证：∠BCO=∠D；

(2)、若CD=4 $\sqrt{2}$ ，OE=1，求⊙O的半径．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - 3 x + 2 a - 1 = 0$ 有两个不相等的实数根．

(1)、求a的取值范围；

(2)、若a为正整数，求方程的根．

查看试题解析
23. 某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w（双）与销售单价x（元）满足w＝﹣2x+80（20≤x≤40），设销售这种手套每天的利润为y（元）．

(1)、求y与x之间的函数关系式；

(2)、当销售单价定为多少元时，每天的利润最大？最大利润是多少？

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} - 4 x - 1$ 与y轴交于点A，其对称轴与x轴交于点B，一次函数 $y = k x + b (k \neq 0)$ 的图象经过点A，B．

(1)、求一次函数的表达式；

(2)、当 $x > - 3$ 时，对于x的每一个值，函数 $y = n x (n \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出n的取值范围．

查看试题解析
25. 已知：如图，在 $△ A B C$ 中， $A B = A C$ ， D是BC的中点．以BD为直径作 $⊙ O$ ，交边AB于点P，连接PC，交AD于点E．

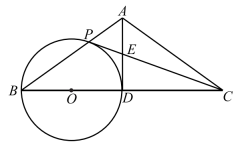(1)、求证：AD是 $⊙ O$ 的切线；

(2)、若PC是 $⊙ O$ 的切线， $B C = 8$ ，求PC的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，二次函数 $y = x^{2} + b x + c$ 的图象经过点（0， $- 3$ ），（3，0）．

(1)、求二次函数的表达式；

(2)、将二次函数 $y = x^{2} + b x + c$ 的图象向上平移 $n (n > 0)$ 个单位后得到的图象记为G，当 $0 \leq x \leq \frac{5}{2}$ 时，图象G与x轴只有一个公共点，结合函数的图象，直接写出n的取值范围．

查看试题解析
27. 如图，在等腰 $△ A B C$ 中， $∠ B A C = 90 °$ ，点D在线段BC的延长线上，连接AD ，将线段AD绕点A逆时针旋转90°得到线段AE，连接CE，射线BA与CE相交于点F．

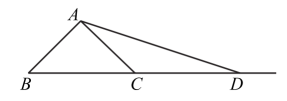(1)、依题意补全图形；

(2)、用等式表示线段BD 与CE的数量关系，并证明；

(3)、若F为CE中点， $A B = \sqrt{2}$ ，则CE的长为．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，点M在x轴上，以点M为圆心的圆与x轴交于 $A (1 ， 0)$ ， $B (4 ， 0)$ 两点，对于点Р和 $⊙ M$ ，给出如下定义：若抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过A，B两点且顶点为P，则称点Р为 $⊙ M$ 的“图象关联点”．

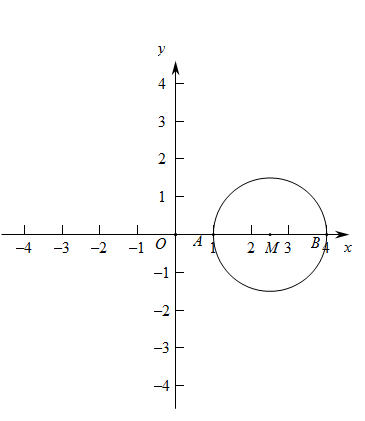(1)、已知 $E (5 ， 2)$ ， $F (\frac{5}{2} ， - 4)$ ， $G (3 ， 1)$ ， $H (\frac{5}{2} ， 3)$ ，在点E，F，G，H中， $⊙ M$ 的”图象关联点”是；

(2)、已知 $⊙ M$ 的“图象关联点”P在第一象限，若 $O P = \frac{5}{3} P M$ ，判断OP与 $⊙ M$ 的位置关系，并证明；

(3)、已知 $C (4 ， 2)$ ， $D (1 ， 2)$ ，当 $⊙ M$ 的“图象关联点”Р在 $⊙ M$ 外且在四边形ABCD内时，直接写出抛物线 $y = a x^{2} + b x + c$ 中a的取值范围．

查看试题解析