北京市朝阳区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 随着2022年北京冬奥会日渐临近，我国冰雪运动发展进入快车道，取得了长足进步．在此之前，北京冬奥组委曾面向全球征集2022年冬奥会会徵和冬残奥会会徽设计方案，共收到设计方案4506件，以下是部分参选作品，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，四边形ABCD内接于 $⊙ O$ ，若 $∠ C = 130 °$ ，则 $∠ B O D$ 的度数为（）

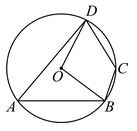A、50° B、100° C、130° D、150°

查看试题解析
3. 对于二次函数 $y = - {(x - 1)}^{2}$ 的图象的特征，下列描述正确的是（）

A、开口向上 B、经过原点 C、对称轴是y轴 D、顶点在x轴上

查看试题解析
4. 若关于x的一元二次方程 $(a - 1) x^{2} + a^{2} x - a = 0$ 有一个根是 $x = 1$ ，则a的值为（）

A、-1 B、0 C、1 D、-1或1

查看试题解析
5. 如图，A，B，C是正方形网格中的三个格点，则 $\overset{⌢}{A B C}$ 是（）

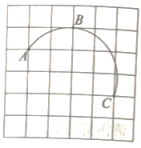A、优弧 B、劣弧 C、半圆 D、无法判断

查看试题解析
6. 参加一次活动的每个人都和其他人各握了一次手，所有人共握手10次，有多少人参加活动？设有x人参加活动，可列方程为（）

A、 $\frac{1}{2} x (x - 1) = 10$ B、 $x (x - 1) = 10$ C、 $\frac{1}{2} x (x + 1) = 10$ D、 $2 x (x - 1) = 10$

查看试题解析
7. 投掷一枚质地均匀的硬币m次，正面向上n次，下列表达正确的是（）

A、 $\frac{n}{m}$ 的值一定是 $\frac{1}{2}$ B、 $\frac{n}{m}$ 的值一定不是 $\frac{1}{2}$ C、m越大， $\frac{n}{m}$ 的值越接近 $\frac{1}{2}$ D、随着m的增加， $\frac{n}{m}$ 的值会在 $\frac{1}{2}$ 附近摆动，呈现出一定的稳定性

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ ，当 $- 1 \leq x \leq 1$ 时，总有 $- 1 \leq y \leq 1$ ，有如下几个结论：
①当 $b = c = 0$ 时， $| a | \leq 1$ ；
②当 $a = 1$ 时，c的最大值为0；
③当 $x = 2$ 时，y可以取到的最大值为7．
上述结论中，所有正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

9. 在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是

查看试题解析
10. 将抛物线 $y = 2 x^{2}$ 向上平移一个单位长度，得到的抛物线的表达式为．

查看试题解析
11. 若一个正多边形的边长等于它的外接圆的半径，则这个正多边形是正边形．

查看试题解析
12. 用一个半径为2的半圆作一个圆锥的侧面，这个圆锥的底面圆的半径为．

查看试题解析
13. 某件商品的销售利润y（元）与商品销售单价x（元）之间满足 $y = - x^{2} + 6 x - 7$ ，不考虑其他因素，销售一件该商品的最大利润为元．

查看试题解析
14. 如图，一个可以自由转动且质地均匀的转盘，被分成6个大小相同的扇形，指针是固定的，当转盘停止时，指针指向任意一个扇形的可能性相同（指针指向两个扇形的交线时，当作指向右边的扇形）．把部分扇形涂上了灰色，则指针指向灰色区域的概率为．

查看试题解析
15. 抛物线 $y = a x^{2} + b x + c$ 的对称轴及部分图象如图所示，则关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的两根为．

查看试题解析
16. 为了落实“双减”政策，朝阳区一些学校在课后服务时段开设了与冬奥会项目冰壶有关的选修课．如图，在冰壶比赛场地的一端画有一些同心圆作为营垒，其中有两个圆的半径分别约为60cm和180 cm，小明掷出一球恰好沿着小圆的切线滑行出界，则该球在大圆内滑行的路径MN的长度为cm．

查看试题解析

三、解答题

17. 解方程： $2 x^{2} - 9 x + 10 = 0$ ．

查看试题解析
18. 已知：如图，A为 $⊙ O$ 上的一点．
求作：过点A且与 $⊙ O$ 相切的一条直线．
作法：①连接OA；
②以点A为圆心，OA长为半径画弧，与 $⊙ O$ 的一个交点为B，作射线OB；
③以点B为圆心，OA长为半径画弧，交射线OB于点P（不与点O重合）；
④作直线PA．
直线PA即为所求．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接BA．
由作法可知 $B O = B A = B P$ ．
∴点A在以OP为直径的圆上．
∴ $∠ O A P = 90 °$ （）（填推理的依据）．
∵OA是 $⊙ O$ 的半径，
∴直线PA与 $⊙ O$ 相切（）（填推理的依据）．

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - (a + 2) x + a + 1 = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、若方程的两个根都是正整数，求a的最小值．

查看试题解析
20. 小明在画一个二次函数的图象时，列出了下面几组y与x的对应值．
x
…
$- 2$
$- 1$
0
1
2
…
y
…
3
4
3
0
$- 5$
…

(1)、求该二次函数的表达式；

(2)、该二次函数的图象与直线 $y = n$ 有两个交点A，B，若 $A B > 6$ ，直接写出n的取值范围．

查看试题解析
21. 一个不透明的袋中装有2个红球、1个白球，这些球除颜色外，没有任何其他区别．有如下两个活动：
活动1：从袋中随机摸出一个球，记录下颜色，然后从袋中剩余的球中再随机摸出一个球，摸出的两个球都是红球的概率记为 $P_{1}$ ；
活动2：从袋中随机摸出一个球，记录下颜色，然后把这个球放回袋中并摇匀，重新从袋中随机摸出一个球，两次摸出的球都是红球的概率记为 $P_{2}$ ．
请你猜想 $P_{1}$ ， $P_{2}$ 的大小关系，并用画树状图或列表的方法列出所有可能的结果，验证你的猜想．

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， O为AC上一点，以点O为圆心，OC为半径的圆恰好与AB相切，切点为D， $⊙ O$ 与AC的另一个交点为E．

(1)、求证：BO平分 $∠ A B C$ ；

(2)、若 $∠ A = 30 °$ ， $A E = 1$ ，求BO的长．

查看试题解析
23. 在等边 $△ A B C$ 中，将线段AB绕点A顺时针旋转 $α (0 ° < α < 180 °)$ 得到线段AD．

(1)、若线段DA的延长线与线段BC相交于点E（不与点B，C重合），写出满足条件的α的取值范围；

(2)、在（1）的条件下连接BD，交CA的延长线于点F．
①依题意补全图形；
②用等式表示线段AE，AF，CE之间的数量关系，并证明．

查看试题解析
24. 在平面直角坐标系xOy中，点 $(- 1 ， y_{1})$ ， $(1 ， y_{2})$ ， $(2 ， y_{3})$ 在抛物线 $y = a x^{2} + b x$ 上．

(1)、若 $a = 1$ ， $b = - 2$ ，求该抛物线的对称轴并比较 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小；

(2)、已知抛物线的对称轴为 $x = t$ ，若 $y_{2} < 0 < y_{3} < y_{1}$ ，求t的取值范围．

查看试题解析
25. 对于平面直角坐标系xOy中的图形M和点P给出如下定义：Q为图形M上任意一点，若P，Q两点间距离的最大值和最小值都存在，且最大值是最小值的2倍，则称点P为图形M的“二分点”．
已知点N（3，0），A（1，0）， $B (0 ， \sqrt{3})$ ， $C (\sqrt{3} ， - 1)$ ．

(1)、①在点A，B，C中，线段ON的“二分点”是；
②点D（a，0），若点C为线段OD的“二分点”，求a的取值范围；

(2)、以点O为圆心，r为半径画圆，若线段AN上存在 $⊙ O$ 的“二分点”，直接写出r的取值范围．

查看试题解析

x	…	$- 2$	$- 1$	0	1	2	…
y	…	3	4	3	0	$- 5$	…