北京市昌平区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-26 类型：期末考试

进入出卷网下载

一、单选题

1. 已知∠A为锐角，且sinA＝ $\frac{1}{2}$ ，那么∠A等于（　　）

A、15° B、30° C、45° D、60°

查看试题解析
2. 已知 $3 a = 4 b (a b \neq 0)$ ，则下列各式正确的是（）

A、 $\frac{a}{b} = \frac{4}{3}$ B、 $\frac{a}{b} = \frac{3}{4}$ C、 $\frac{a}{3} = \frac{b}{4}$ D、 $\frac{a}{3} = \frac{4}{b}$

查看试题解析
3. 抛物线y＝x²﹣2的顶点坐标是（）

A、（0，﹣2） B、（﹣2，0） C、（0，2） D、（2，0）

查看试题解析
4. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A (2 ， 3)$ ，则k的值为（）

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
5. 如图，AD是△ABC的外接圆⊙O的直径，若∠BCA＝50°，则∠BAD＝（　　）

A、30° B、40° C、50° D、60°

查看试题解析
6. 如图，面积为18的正方形ABCD内接于⊙O，则⊙O的半径为（）

A、 $\frac{3}{2}$ B、 $\frac{3}{2} \sqrt{2}$ C、3 D、 $3 \sqrt{2}$

查看试题解析
7. 关于二次函数y=-（x -2）²＋3，以下说法正确的是（）

A、当x＞-2时，y随x增大而减小 B、当x＞-2时，y随x增大而增大 C、当x＞2时，y随x增大而减小 D、当x＞2时，y随x增大而增大

查看试题解析
8. 如图，在平面直角坐标系 $x O y$ 中，⊙O的半径为2，与x轴，y轴的正半轴分别交于点A，B，点C（1，c），D（ $\sqrt{2}$ ， d），E（e，1），P（m，n）均为 $\overset{⌢}{A B}$ 上的点（点P不与点A，B重合），若m＜n＜ $\sqrt{3}$ m，则点P的位置为（）

A、在 $\overset{⌢}{B C}$ 上 B、在 $\overset{⌢}{C D}$ 上 C、在 $\overset{⌢}{D E}$ 上 D、在 $\overset{⌢}{E A}$ 上

查看试题解析

二、填空题

9. 请写出一个开口向下，并且与y轴交于点（0，1）的抛物线的表达式

查看试题解析
10. 已知⊙O的半径为5cm，圆心O到直线l的距离为4cm，那么直线l与⊙O的位置关系是．

查看试题解析
11. 若扇形的圆心角为60°，半径为2，则该扇形的弧长是（结果保留 $π$ ）

查看试题解析
12. 点A（-1，y₁），B（4，y₂）是二次函数y＝（x－1）²图象上的两个点，则y₁y₂（填“＞”，“＜”或“＝”）

查看试题解析
13. 如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB=10，CD=8，则OH的长为

查看试题解析
14. 已知反比例函数y＝ $\frac{m - 1}{x}$ 的图象分布在第二、四象限，则m的取值范围是

查看试题解析
15. 如图，PA，PB分别与⊙O相切于A，B两点，C是优弧AB上的一个动点，若∠P = 50°，则∠ACB ＝°

查看试题解析
16. 点A（x₁ ， y₁），B（x₂ ， y₂）（x₁·x₂≥0）是y=ax²（a≠0）图象上的点，存在 $| x_{1} - x_{2} |$ =1时， $| y_{1} - y_{2} |$ =1成立，写出一个满足条件a的值

查看试题解析

三、解答题

17. 计算： 2sin60°+tan45°－cos30°tan60°

查看试题解析
18. 如图，在△ABC中，∠C=90°，AC=4，AB=5，点D在AC上且AD=3，DE⊥AB于点E，求AE的长

查看试题解析
19. 已知：二次函数y=x²－4x+3

(1)、求出二次函数图象的顶点坐标及与x轴交点坐标；

(2)、在坐标系中画出图象，并结合图象直接写出y＜0时，自变量x的取值范围

查看试题解析
20. 如图，在△ABC中，∠B＝30°，AB＝4，AD⊥BC于点D且tan∠CAD＝ $\frac{1}{2}$ ，求BC的长

查看试题解析
21. 已知：如图，△ABC为锐角三角形，AB＝AC
求作：一点P，使得∠APC＝∠BAC
作法：①以点A为圆心， AB长为半径画圆；
②以点B为圆心，BC长为半径画弧，交⊙A于点C，D两点；
③连接DA并延长交⊙A于点P
点P即为所求

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明
证明：连接PC，BD
∵AB＝AC，
∴点C在⊙A上
∵BC＝BD，
∴∠ ▲ ＝∠ ▲
∴∠BAC＝ $\frac{1}{2}$ ∠CAD
∵点D，P在⊙A上，
∴∠CPD＝ $\frac{1}{2}$ ∠CAD（）（填推理的依据）
∴∠APC＝∠BAC

查看试题解析
22. 如图，在平面直角坐标系xOy中，A（a，2）是一次函数 $y = x - 1$ 的图象与反比例函数 $y = \frac{k}{x} （ k \neq 0 ）$ 的图象的交点

(1)、求反比例函数 $y = \frac{k}{x} （ k \neq 0 ）$ 的表达式；

(2)、过点P（n，0）且垂直于x轴的直线与一次函数图象，反比例函数图象的交点分别为M，N，当S_△_OPM＞S_△_OPN时，直接写出n的取值范围

查看试题解析
23. 居庸关位于距北京市区50余公里外的昌平区境内，是京北长城沿线上的著名古关城，有“天下第一雄关”的美誉某校数学社团的同学们使用皮尺和测角仪等工具，测量南关主城门上城楼顶端距地面的高度，下表是小强填写的实践活动报告的部分内容：请你帮他计算出城楼的高度AD（结果精确到0.1m，sin35°≈0.574，cos35°≈0.819，tan35°≈0.700）
题目
测量城楼顶端到地面的高度
测量目标示意图
相关数据
BM=16m， BC=13m，∠ABC=35°，∠ACE=45°

查看试题解析
24. 如图，⊙O是△ABC的外接圆，AB是⊙O的直径，AB⊥CD于点E，P是AB延长线上一点，且∠BCP＝∠BCD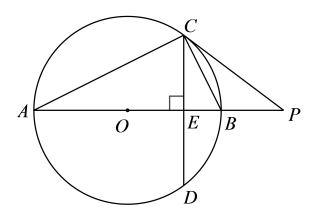

(1)、求证：CP是⊙O的切线；

(2)、连接DO并延长，交AC于点F，交⊙O于点G，连接GC若⊙O的半径为5，OE＝3，求GC和OF的长

查看试题解析
25. 随着冬季的到来，干果是这个季节少不了的营养主角，某超市购进一批干果，分装成营养搭配合理的小包装后出售，每袋成本20元销售过程中发现，每天销售量y（袋）与销售单价x（元）之间的关系可近似地看作一次函数：y＝-2x＋80（20≤x≤40），设每天获得的利润为w（元）

(1)、求出w与x的关系式；

(2)、当销售单价定为多少元时，每天可获得最大利润？最大利润是多少？

查看试题解析
26. 在平面直角坐标系xOy中，点（1，m）和点（3，n）在二次函数y＝x²＋bx的图象上

(1)、当m＝-3时
①求这个二次函数的顶点坐标；
②若点（-1，y₁），（a，y₂）在二次函数的图象上，且y₂＞y₁ ，则a的取值范围是 ▲ ；

(2)、当mn＜0时，求b的取值范围

查看试题解析
27. 已知∠POQ=120°，点A，B分别在OP，OQ上，OA＜OB，连接AB，在AB上方作等边△ABC，点D是BO延长线上一点，且AB=AD，连接AD
备用图

(1)、补全图形；

(2)、连接OC，求证：∠COP=∠COQ；

(3)、连接CD，CD交OP于点F，请你写出一个∠DAB的值，使CD=OB+OC一定成立，并证明

查看试题解析
28. 在平面直角坐标系xOy中，对于点P，O，Q给出如下定义：若OQ＜PO＜PQ且PO≤2，我们称点P是线段OQ的“潜力点”
已知点O（0，0），Q（1，0）

(1)、在P₁（0，-1），P₂（ $\frac{1}{2}$ ， $\frac{3}{2}$ ），P₃（-1，1）中是线段OQ的“潜力点”是；

(2)、若点P在直线y＝x上，且为线段OQ的“潜力点”，求点P横坐标的取值范围；

(3)、直线y＝2x＋b与x轴交于点M，与y轴交于点N，当线段MN上存在线段OQ 的“潜力点”时，直接写出b的取值范围

查看试题解析

题目	测量城楼顶端到地面的高度
测量目标示意图
相关数据	BM=16m， BC=13m，∠ABC=35°，∠ACE=45°