2021-2022学年浙教版数学九下3.4 简单几何体的表面展开图同步练习
试卷更新日期:2022-01-26 类型:同步测试
一、单选题
-
1. 一个几何体的展开图如图所示,则这个几何体是( )
 A、三棱柱 B、三棱锥 C、四棱锥 D、圆锥2. 下列各图中,可以是一个正方体的平面展开图的是( )A、
A、三棱柱 B、三棱锥 C、四棱锥 D、圆锥2. 下列各图中,可以是一个正方体的平面展开图的是( )A、 B、
B、 C、
C、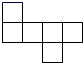 D、
D、 3. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,则在原正方体中,与“展”字所在面相对面上的汉字是( )
3. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,则在原正方体中,与“展”字所在面相对面上的汉字是( ) A、长 B、春 C、新 D、区4. 近年来,我省奋力建设“生态环境”,为此欣欣特别制作了一个正方体玩具,其展开图如图所示,则原正方体中与“环”字相对的字是( )
A、长 B、春 C、新 D、区4. 近年来,我省奋力建设“生态环境”,为此欣欣特别制作了一个正方体玩具,其展开图如图所示,则原正方体中与“环”字相对的字是( ) A、建 B、设 C、生 D、态5. 下图各图中,是正方体展开图的是( )A、
A、建 B、设 C、生 D、态5. 下图各图中,是正方体展开图的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧 , 交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
6. 如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧 , 交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( ) A、2 B、 C、4 D、7. 下列图形中不是正方体展开图的是( )
A、2 B、 C、4 D、7. 下列图形中不是正方体展开图的是( )
A、 B、
B、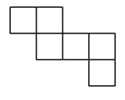 C、
C、 D、
D、 8. 下列各图中,经过折叠能围成一个正方体的是( )A、
8. 下列各图中,经过折叠能围成一个正方体的是( )A、 B、
B、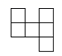 C、
C、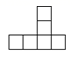 D、
D、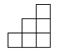 9. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )
9. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是( )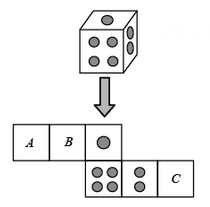 A、 代表
A、 代表 B、 代表
B、 代表  C、 代表
C、 代表  D、 代表
D、 代表  10. 用如图所示的平面图形可以围成正方体,则与 点重合的点是( )
10. 用如图所示的平面图形可以围成正方体,则与 点重合的点是( ) A、点 B、点 C、点 D、点
A、点 B、点 C、点 D、点二、填空题
-
11. 圆锥的母线长为5,高为3,侧面积为 .12. 用一个半径为8,圆心角为90°的扇形围成一个圆锥的侧面,则圆锥的高为 .13. 圆锥的侧面积为 , 底面圆半径为3cm.则圆锥的母线长为cm.14. 小华为参加元旦晚会演出,准备制作一顶圆锥形彩色纸帽,如果纸帽的侧面展开图是半径为 , 圆心角为的扇形,则此圆锥底面圆的半径为 .15. 如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“答”字相对的面上的字是.
 16. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)
16. 如图,是一个多面体的表面展开图,每个面内都标注了字母,如果面A在多面体的底部,那么从上面看是面 . (填字母)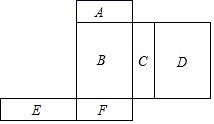
三、综合题
-
17. 如图所示是一个正方体的表面展开图,请回答下列问题:
 (1)、与面A相对的面是 , 与面B相对的面是 , 与面C相对的面是;(2)、若 , , , ,且相对两个面所表的代数式的和都相等,分别求D , F代表的代数式.18. 已知如图,扇形AOB的圆心角为120°,半径OA为9cm.
(1)、与面A相对的面是 , 与面B相对的面是 , 与面C相对的面是;(2)、若 , , , ,且相对两个面所表的代数式的和都相等,分别求D , F代表的代数式.18. 已知如图,扇形AOB的圆心角为120°,半径OA为9cm. (1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.19. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.19. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: (1)、小明总共剪开了条棱.(直接写出答案)(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、据小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是88cm,求这个长方体纸盒的体积.20. 如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
(1)、小明总共剪开了条棱.(直接写出答案)(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、据小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是88cm,求这个长方体纸盒的体积.20. 如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题: (1)、如果A面在长方体的底部,那么哪一个面会在上面?(2)、如果F面在前面,B面在左面,那么哪一个面会在上面?(字母朝外)21. 如图,半圆形薄铁皮的直径AB=8,点O为圆心(不与A , B重合),连接AC并延长到点D , 使AC=CD , 作DH⊥AB , 交半圆、BC于点E , F , 连接OC , ∠ABC=θ,θ随点C的移动而变化.
(1)、如果A面在长方体的底部,那么哪一个面会在上面?(2)、如果F面在前面,B面在左面,那么哪一个面会在上面?(字母朝外)21. 如图,半圆形薄铁皮的直径AB=8,点O为圆心(不与A , B重合),连接AC并延长到点D , 使AC=CD , 作DH⊥AB , 交半圆、BC于点E , F , 连接OC , ∠ABC=θ,θ随点C的移动而变化.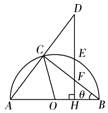 (1)、移动点C , 当点H , B重合时,求证:AC=BC;(2)、当θ<45°时,求证:BH•AH=DH•FH;(3)、当θ=45°时,将扇形OAC剪下并卷成一个圆锥的侧面,求该圆锥的底面半径和高.22. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1.
(1)、移动点C , 当点H , B重合时,求证:AC=BC;(2)、当θ<45°时,求证:BH•AH=DH•FH;(3)、当θ=45°时,将扇形OAC剪下并卷成一个圆锥的侧面,求该圆锥的底面半径和高.22. 某工厂要加工一批上下底密封纸盒,设计者给出了密封纸盒的三视图,如图1. (1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)23. 如图,在平面直角坐标系中, 为直角三角形, , ,按要求解答下列问题:
(1)、由三视图可知,密封纸盒的形状是;(2)、根据该几何体的三视图,在图2中补全它的表面展开图;(3)、请你根据图1中数据,计算这个密封纸盒的表面积.(结果保留根号)23. 如图,在平面直角坐标系中, 为直角三角形, , ,按要求解答下列问题: (1)、以原点 为位似中心画出 ,使它与 的相似比为3:2(2)、将 绕点 顺时针旋转90°,画出旋转后的(3)、用点 旋转到点 所经过的路径与 、 围成的扇形做成一个圆锥的侧面(接缝忽略不计),求这个圆锥的高.(保留精确值)24. 如图,已知圆柱底面的直径 ,圆柱的高 ,在圆柱的侧面上,过点 , 嵌有一圈长度最短的金属丝.(1)、现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是______.A、
(1)、以原点 为位似中心画出 ,使它与 的相似比为3:2(2)、将 绕点 顺时针旋转90°,画出旋转后的(3)、用点 旋转到点 所经过的路径与 、 围成的扇形做成一个圆锥的侧面(接缝忽略不计),求这个圆锥的高.(保留精确值)24. 如图,已知圆柱底面的直径 ,圆柱的高 ,在圆柱的侧面上,过点 , 嵌有一圈长度最短的金属丝.(1)、现将圆柱侧面沿 剪开,所得的圆柱侧面展开图是______.A、 ;
B、
;
B、 ;
C、
;
C、 ;
D、
;
D、 (2)、求该长度最短的金属丝的长.
(2)、求该长度最短的金属丝的长. 25. 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
25. 如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C. (1)、请完成如下操作:
(1)、请完成如下操作:①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD.
(2)、请在(1)的基础上,完成下列填空:①写出点的坐标:C_▲__;D(_▲_);
②⊙D的半径=_▲_(结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面的面积为_▲_;(结果保留π)
④若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由.
26. 如图是一个正方体纸盒的表面展开图,纸盒中相对两个面上的数互为倒数.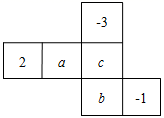 (1)、填空: , ;(2)、先化简,再求值: .
(1)、填空: , ;(2)、先化简,再求值: .

