第二十七章 相似----人教版九年级下册同步练习
试卷更新日期:2022-01-25 类型:单元试卷
一、单选题
-
1. 已知x:y=5:2,则下列各式中错误的是( )A、 B、 C、 D、2. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
 A、1 B、2 C、3 D、43. 在下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D,∠B=∠E B、=且∠B=∠E C、== D、=且∠A=∠D4. 如图,在中,点D,E分别在的边AB,AC上,如果添加一个条件,不一定能使与相似,那么这个条件可能是( )
A、1 B、2 C、3 D、43. 在下列条件中,不能判断△ABC与△DEF相似的是( )A、∠A=∠D,∠B=∠E B、=且∠B=∠E C、== D、=且∠A=∠D4. 如图,在中,点D,E分别在的边AB,AC上,如果添加一个条件,不一定能使与相似,那么这个条件可能是( ) A、 B、 C、 D、5. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的面积是1,则四边形BCED的面积是( )
A、 B、 C、 D、5. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的面积是1,则四边形BCED的面积是( ) A、1 B、2 C、3 D、46. 如图,下列选项中不能判定△ACD∽△ABC的是( )
A、1 B、2 C、3 D、46. 如图,下列选项中不能判定△ACD∽△ABC的是( ) A、∠ACD=∠B B、∠ADC=∠ACB C、AC2=AD•AB D、BC2=BD•AB7. 如图,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB、AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
A、∠ACD=∠B B、∠ADC=∠ACB C、AC2=AD•AB D、BC2=BD•AB7. 如图,在△ABC 中,∠C=90°,BC=6,D,E 分别在 AB、AC上,将△ABC沿DE折叠,使点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) A、 B、2 C、3 D、48. 如图,已知直线l1∥l2 , l1、l2之间的距离AE为 ,在△ABC中,BC=2,AB= ,将△ABC绕点C在平面内顺时针旋转得到△A′B′C,若旋转角为60°,A′C交直线l2于点D,则CD的长度为( )
A、 B、2 C、3 D、48. 如图,已知直线l1∥l2 , l1、l2之间的距离AE为 ,在△ABC中,BC=2,AB= ,将△ABC绕点C在平面内顺时针旋转得到△A′B′C,若旋转角为60°,A′C交直线l2于点D,则CD的长度为( ) A、 B、 C、 D、 ﹣
A、 B、 C、 D、 ﹣二、填空题
-
9. 已知a=4,b=9,则这两个数a,b的比例中项为 .10. 如图,AB和DE是直立在地面上的两根立柱,AB=4m,AB在阳光下的影长BC=3m,在同一时刻阳光下DE的影长EF=4m,则DE的长为 米.
 11. 如图, 中,点D在边 上,且 ,若 , ,则 的长为 .
11. 如图, 中,点D在边 上,且 ,若 , ,则 的长为 . 12. 如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
12. 如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 . 13. 如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是 .
13. 如图,在平面直角坐标系xOy中,△ABC与△A′B′C′顶点的横、纵坐标都是整数.若△ABC与△A′B′C′是位似图形,则位似中心的坐标是 . 14. 如图,在平面直角坐标系中,点、的坐标分别为、 , 点在第一象限内,连接、.已知 , 则.
14. 如图,在平面直角坐标系中,点、的坐标分别为、 , 点在第一象限内,连接、.已知 , 则.
三、作图题
-
15. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B、C、D均在格点上在图②、图③中,只用无刻度的直尺,在给定的正方形网格中,按要求画图,保留作图痕迹,不要求写出画法.
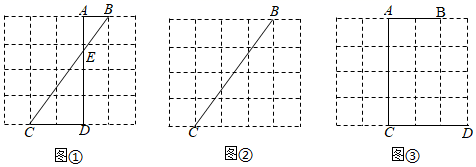 (1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .
(1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .四、解答题
-
16. 在四边形ABCD中, , , , , 的平分线分别交AD、AC于点E、F,求 的值.
 17. 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论.
17. 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论. 18. 两棵树的高度分别是 16.6米, 13.6米,两棵树的根部之间的距离AC=7米.小强沿着正对这两棵树的方向从右向左前进,如果小强的眼睛与地面的距离为1.6米,当小强与树 的距离等于多少时,小强的眼睛与树 、 的顶部 、 恰好在同一条直线上,请说明理由.
18. 两棵树的高度分别是 16.6米, 13.6米,两棵树的根部之间的距离AC=7米.小强沿着正对这两棵树的方向从右向左前进,如果小强的眼睛与地面的距离为1.6米,当小强与树 的距离等于多少时,小强的眼睛与树 、 的顶部 、 恰好在同一条直线上,请说明理由.
五、综合题
-

