2021-2022学年浙教版数学九下2.3 三角形的内切圆同步练习
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 一直角三角形的斜边长为c,其内切圆半径是r,则三角形面积与其内切圆的面积之比是( )A、 B、 C、 D、2. 如图所示,已知⊙I是△ABC的内切圆,点I是内心,若∠A=35°,则∠BIC等于( )
 A、35° B、70° C、145° D、107.5°3. 如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( )
A、35° B、70° C、145° D、107.5°3. 如图,在 中, 平分 ,使用尺规作射线 ,与 交于点 ,下列判断正确的是( ) A、 平分 B、 C、点 是 的内心 D、点 到点 , , 的距离相等4. 利用尺规作一个任意三角形的内心 ,以下作法正确的是( )A、
A、 平分 B、 C、点 是 的内心 D、点 到点 , , 的距离相等4. 利用尺规作一个任意三角形的内心 ,以下作法正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,点 为 的内心, , , ,则 的面积是( )
5. 如图,点 为 的内心, , , ,则 的面积是( ) A、 B、 C、2 D、46. 如图,在 中, 其周长为20,⊙I是 的内切圆,其半径为 ,则 的外接圆半径为( )
A、 B、 C、2 D、46. 如图,在 中, 其周长为20,⊙I是 的内切圆,其半径为 ,则 的外接圆半径为( ) A、7 B、 C、 D、7. 如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )
A、7 B、 C、 D、7. 如图所示,在4×4的网格中,A、B、C、D、O均在格点上,则点O是( )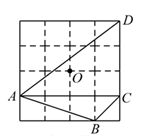 A、△ABC的内心 B、△ABC的外心 C、△ACD的外心 D、△ACD的重心8. 如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )
A、△ABC的内心 B、△ABC的外心 C、△ACD的外心 D、△ACD的重心8. 如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )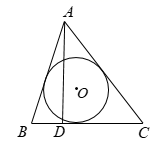 A、 B、 C、 D、9. 如图,在 中, .小丽按照下列方法作图:
A、 B、 C、 D、9. 如图,在 中, .小丽按照下列方法作图:①作 的角平分线 ,交 于点D;
②作 的垂直平分线,交 于点E .
根据小丽画出的图形,判断下列说法中正确的是( )
 A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等10. ⊙O为△ABC的内切圆,那么点O是△ABC的( )A、三条中线交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线交点
A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等10. ⊙O为△ABC的内切圆,那么点O是△ABC的( )A、三条中线交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线交点二、填空题
-
11. 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,则AF的长为 .
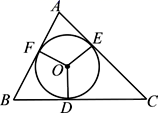 12. 如图,在四边形 中, .若 ,则 的内切圆面积(结果保留 ).
12. 如图,在四边形 中, .若 ,则 的内切圆面积(结果保留 ).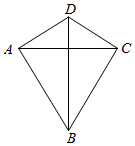 13. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为.
13. 如图,已知 的半径为2,弦 ,点 为优弧 上动点,点 为 的内心,当点 从点 向点 运动时,点 移动的路径长为. 14. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .
14. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .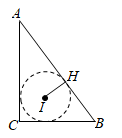 15. 已知△ABC 的三边之和为m,S△ABC=S,则它的内心到各边的距离均为.16. 如图,边长为 的等边△ABC的内切圆的半径为.
15. 已知△ABC 的三边之和为m,S△ABC=S,则它的内心到各边的距离均为.16. 如图,边长为 的等边△ABC的内切圆的半径为.
三、综合题
-
17. 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心(三角形三个内角平分线的交点),连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE
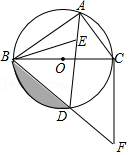 (1)、求证:DB=DE(2)、求证:直线CF为⊙O的切线(3)、若CF=4,求图中阴影部分的面积18. 如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C.
(1)、求证:DB=DE(2)、求证:直线CF为⊙O的切线(3)、若CF=4,求图中阴影部分的面积18. 如图,开口向上的抛物线y=ax2﹣2ax﹣3a与X轴相交于点A、B(点A在点B的左侧),顶点为D.经过点A的直线y=kx+b(k>0)与抛物线的另一个交点为C. (1)、求点C的坐标(用含a、k的代数式表示).(2)、当△ACD的内心恰在X轴上时,求 得值.(3)、已知△ADB为直角三角形:
(1)、求点C的坐标(用含a、k的代数式表示).(2)、当△ACD的内心恰在X轴上时,求 得值.(3)、已知△ADB为直角三角形:①a的值等于 (直接写出结果).
②若直线AC下方的拋物线上存在点P,使△APC∽△ADB,求k的值及点P的坐标.
19. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交点)为顶点的 ,且 . (1)、将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .(2)、设 的内切圆的半径为 , 的外接圆的半径为 ,则 .20. 阅读以下材料,并按要求完成相应地任务:
(1)、将 绕点 顺时针旋转90°后得到 (其中 三点旋转后的对应点分别是 ),画出 .(2)、设 的内切圆的半径为 , 的外接圆的半径为 ,则 .20. 阅读以下材料,并按要求完成相应地任务:

莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则 .
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴ ,
∴ ①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴ ,∴ ②,
任务:
(1)、观察发现: , (用含R,d的代数式表示);(2)、请判断BD和ID的数量关系,并说明理由;(3)、请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;(4)、应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为cm.21. 如图,点 是 的内心, 的延长线和 的外接圆 相交于点 ,过 作直线 . (1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的半径.22. 有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.
(1)、求证: 是 的切线;(2)、求证: ;(3)、若 , ,求 的半径.22. 有一组邻边相等且对角互补的四边形叫做等邻边互补四边形. (1)、如图1,在等邻边互补四边形ABCD中,AD=CD,且AD//BC, BC=2AD,求∠B的度数;(2)、如图2,四边形ABCD内接于圆O,连结DO交AC于点E (不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;(3)、在(2) 的条件下,延长DO交BC于点F,交圆0于点G,若弧BG=弧AB, tan∠ABC= ,AC=12,求FG的长;(4)、如图3,四边形ABCD内接于圆O,AB=BC, BD为圆0的直径,连结AO并延长交BC于点E,交圆0于点F,连结FC,设tan∠BAF=x, ,求y与x之间的函数关系式.23. 已知直线y= 分别交x轴、y轴于A、B两点.点P从A点出发在x轴上以每秒5个单位的速度向左运动,同时点Q从A点出发沿射线AB以每秒4个单位的速度运动.
(1)、如图1,在等邻边互补四边形ABCD中,AD=CD,且AD//BC, BC=2AD,求∠B的度数;(2)、如图2,四边形ABCD内接于圆O,连结DO交AC于点E (不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;(3)、在(2) 的条件下,延长DO交BC于点F,交圆0于点G,若弧BG=弧AB, tan∠ABC= ,AC=12,求FG的长;(4)、如图3,四边形ABCD内接于圆O,AB=BC, BD为圆0的直径,连结AO并延长交BC于点E,交圆0于点F,连结FC,设tan∠BAF=x, ,求y与x之间的函数关系式.23. 已知直线y= 分别交x轴、y轴于A、B两点.点P从A点出发在x轴上以每秒5个单位的速度向左运动,同时点Q从A点出发沿射线AB以每秒4个单位的速度运动. (1)、试说明:运动过程中PQ始终垂直于AB;(2)、当四边形BOPQ的面积是△ABO面积的一半时,求出发多长时间?(3)、当△APQ的内心恰好在OB上时,求运动时间.24. 在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.
(1)、试说明:运动过程中PQ始终垂直于AB;(2)、当四边形BOPQ的面积是△ABO面积的一半时,求出发多长时间?(3)、当△APQ的内心恰好在OB上时,求运动时间.24. 在△ABC中,∠C= ,⊙O是△ABC的内切圆,⊙P分别与CA的延长线、CB的延长线以及直线AB均相切,⊙O的半径为m,⊙P的半径为n.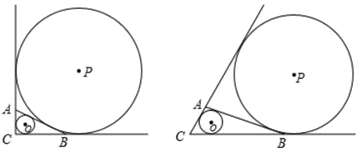 (1)、当 =90°时,AC=6,BC=8时,m= , n=.(2)、当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.25. 如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.
(1)、当 =90°时,AC=6,BC=8时,m= , n=.(2)、当 取下列度数时,求△ABC的面积(用含有m、n的代数式表示,并直接写出答案).①如图, =90°;②如图, =60°.25. 如图,在△ABC中,∠BAC=90°,∠B=60°,AB=2.AD⊥BC于D.E为边BC上的一个(不与B、C重合)点,且AE⊥EF于E,∠EAF=∠B,AF相交于点F.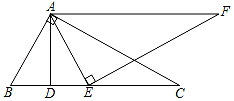 (1)、填空:AC=;∠F= .(2)、当BD=DE时,证明:△ABC≌△EAF.(3)、△EAF面积的最小值是 .(4)、当△EAF的内心在△ABC的外部时,直接写出AE的范围 .26. 阅读以下材料,并按要求完成相应的任务:
(1)、填空:AC=;∠F= .(2)、当BD=DE时,证明:△ABC≌△EAF.(3)、△EAF面积的最小值是 .(4)、当△EAF的内心在△ABC的外部时,直接写出AE的范围 .26. 阅读以下材料,并按要求完成相应的任务:莱昂哈德·欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI =R -2Rr.
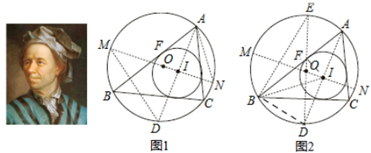
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴ ,∴IA×ID=IM×IN①
如图②,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF
∵DE是⊙O的直径,∴∠DBE=90°.
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴ ,∴ ②,
由(2)知: ,
∴
又∵ ,
∴2Rr=(R+d)(R-d),
∴R -d =2Rr
∴d =R -2Rr
任务:
(1)、观察发现:IM=R+d,IN=(用含R,d的代数式表示);(2)、请判断BD和ID的数量关系,并说明理由.(请利用图1证明)(3)、应用:若△ABC的外接圆的半径为6cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离cm.27. 如图,点 是 的内心, 的延长线和 的外接圆圆 相交于点 ,过 作直线 .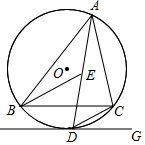 (1)、求证: 是圆 的切线;(2)、若 , ,求优弧 的长.
(1)、求证: 是圆 的切线;(2)、若 , ,求优弧 的长.