第二十六章 反比例函数----人教版九年级下册同步练习
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 下列函数中,y是x的反比例函数的是( ).A、 B、 C、 D、2. 下列各点中,在正比例函数 的图象上的是( )A、 B、(﹣3,﹣1) C、(0,1) D、(6,3)3. 已知一次函数y1=kx-b 与反比例函数y2= ,在同一平面直角坐标系中的图象如图所示,则当kx< +b时,x的取值范围是( )
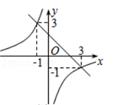 A、x<-1或0<x<3 B、-1<x<0或x>3 C、-3<x<0或x> 1 D、x>34. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A、x<-1或0<x<3 B、-1<x<0或x>3 C、-3<x<0或x> 1 D、x>34. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )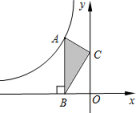 A、3 B、﹣3 C、6 D、﹣65. 函数与在同一直角坐标系中的图象可能是( )A、
A、3 B、﹣3 C、6 D、﹣65. 函数与在同一直角坐标系中的图象可能是( )A、 B、
B、 C、
C、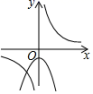 D、
D、 6. 对于函数 , 下列说法错误的是( )A、当时,的值随的增大而增大 B、当时,的值随的增大而减小 C、它的图象分布在第一、三象限 D、它的图象既是轴对称图形又是中心对称图形7. 设 是反比例函数 图象上的任意四点,现有以下结论:
6. 对于函数 , 下列说法错误的是( )A、当时,的值随的增大而增大 B、当时,的值随的增大而减小 C、它的图象分布在第一、三象限 D、它的图象既是轴对称图形又是中心对称图形7. 设 是反比例函数 图象上的任意四点,现有以下结论:①存在无数个四边形 是平行四边形; ②存在无数个四边形 是菱形;
③存在无数个四边形 是矩形; ④至少存在一个四边形 是正方形.
其中正确结论的个数是 ( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,一条直线与反比例函数y= (x>0)的图象交于两点A、B , 与x轴交于点C , 且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y= (x>0)的图象交于两点D、E , 连接DE , 则四边形ABED的面积为( )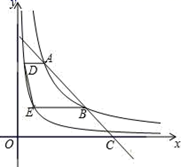 A、4 B、 C、 D、9. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )
A、4 B、 C、 D、9. 设双曲线 (k > 0)与直线y=x交于A,B两点(点A在第三象限),将双曲线在第一象限的一支沿射线BA的方向平移,使其经过点A,将双曲线在第三象限的一支沿射线AB的方向平移,使其经过点B,平移后的两条曲线相交于点P,Q两点,此时我们称平移后的两条曲线所围部分(如图中阴影部分)为双曲线的“眸”,PQ为双曲线的“眸径”.当双曲线 (k > 0)的眸径为4时,k的值为( )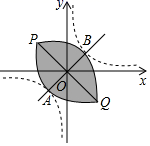 A、 B、 C、2 D、410. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )
A、 B、 C、2 D、410. 如图,直线 与 轴、 轴相交于 , 两点,与 的图象相交于 , 两点,连接 , .下列结论:① ;②不等式 的解集是 或 ;③ ;④ .其中正确的结论是( )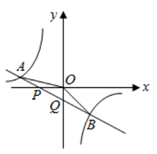 A、①③ B、②③④ C、①③④ D、②④
A、①③ B、②③④ C、①③④ D、②④二、填空题
-
11. 某工程队为教学楼贴瓷砖,已知楼体外表面积为5×103m2.所需的瓷砖块数n与每块瓷砖的面积S(单位:m2)的函数关系式为.12. 已知变量y与x成反比例,当 时, ,则该反比例函数的解析式为.13. 如图,若反比例函数与一次函数交于A、B两点,当时,则x的取值范围是 .
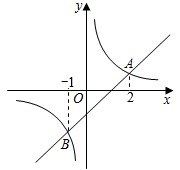 14. 如图,点A在双曲线y=上,点B在双曲线y=上,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为
14. 如图,点A在双曲线y=上,点B在双曲线y=上,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为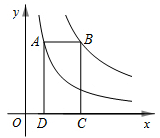 15. 在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y= (m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P , 使得S△ABP=2S△ABO , 那么点P的坐标是 .16. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
15. 在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y= (m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P , 使得S△ABP=2S△ABO , 那么点P的坐标是 .16. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
三、作图题
-
17. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程,在画函数图象时,我们能通过描点或平移的方法画出函数图象.结合上面经历的学习过程,现在来解决下面的问题;
在函数 中,当 时, .
 (1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
(1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.四、解答题
-
18. 已知近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,且400度近视眼镜镜片的焦距为0.25米.小慧原来戴400度的近视眼镜,经过一段时间的矫正治疗后,现在只需戴镜片焦距为0.4米的眼镜了,求小慧所戴眼镜的度数降低了多少度.19. 一枚均匀的正方体骰子,六个面分别标有数字1、2、3、4、5、6,连续抛掷两次,朝上的数字分别是m、n,若把m、n作为点的横、纵坐标,那么点A(m,n)在函数y = 的图象上的概率是多少?20. 如图,一次函数 与反比例函数 图象的两个交点分别为 , , 轴于点 , 轴于点 .
 (1)、根据图象直接回答:在第一象限内,当 取何值时,一次函数值大于反比例函数值;(2)、求一次函数的解析式及 的值;(3)、 是线段 上的一点,连接 , ,若 和 的面积相等,求点 的坐标.
(1)、根据图象直接回答:在第一象限内,当 取何值时,一次函数值大于反比例函数值;(2)、求一次函数的解析式及 的值;(3)、 是线段 上的一点,连接 , ,若 和 的面积相等,求点 的坐标.五、综合题
-
21. 泡茶需要将电热水壶中的水先烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
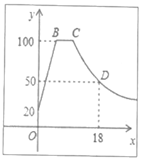 (1)、分别求出图中所对应的函数关系式,并且写出自变量x的取值范围:(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶,问从水烧开到泡茶需要等待多长时间?
(1)、分别求出图中所对应的函数关系式,并且写出自变量x的取值范围:(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶,问从水烧开到泡茶需要等待多长时间?
-