27.4 正多边形与圆----华师大版九年级下册同步试卷
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 如图,正五边形 内接于 ,则 的度数是( )
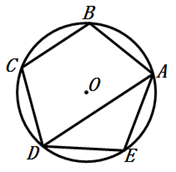 A、36° B、26° C、30° D、45°2. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( )
A、36° B、26° C、30° D、45°2. 如图,⊙O是正五边形ABCDE的外接圆,则正五边形的中心角∠AOB的度数是( ) A、72° B、60° C、54° D、36°3. 在正六边形ABCDEF的中,若BE=10,则这个正六边形外接圆半径是( )
A、72° B、60° C、54° D、36°3. 在正六边形ABCDEF的中,若BE=10,则这个正六边形外接圆半径是( )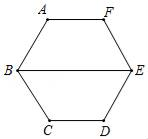 A、 B、5 C、 D、54. 如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接n边形的一边,则n等于( )
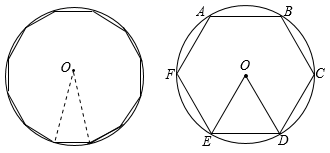
A、 B、5 C、 D、54. 如图,AB、AC分别为⊙O的内接正方形、内接正三边形的边,BC是圆内接n边形的一边,则n等于( )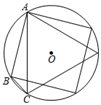 A、8 B、10 C、12 D、165. 我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,AP=2 , 则 =( )
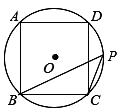
A、8 B、10 C、12 D、165. 我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形ABCDEF是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结AG,CF,AG交CF于点P,AP=2 , 则 =( )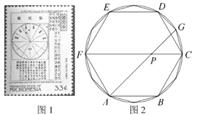 A、2 B、 C、 D、6. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )
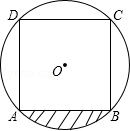
A、2 B、 C、 D、6. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )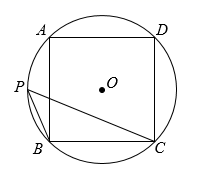 A、 B、 C、 D、7. 一个圆的半径为 ,则该圆的内接正方形的边长为( )A、 B、 C、 D、8. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、 B、 C、 D、7. 一个圆的半径为 ,则该圆的内接正方形的边长为( )A、 B、 C、 D、8. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )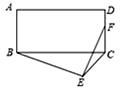 A、 B、4 C、5 D、
A、 B、4 C、5 D、二、填空题
-
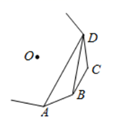
9. 圆内接正六边形的边长为6,则该正六边形的边心距为.10. 如图,A、B、C、D为一个正多边形的相邻四个顶点,O为正多边形的中心,若∠ADB=12°,则这个正多边形的边数为
 11. 如图,已知正六边形 ,连接 ,则 °.
11. 如图,已知正六边形 ,连接 ,则 °.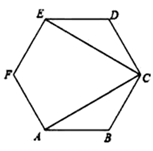 12. 如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正边形.
12. 如图,若以AB为边长作⊙O的内接正多边形,则这个多边形是正边形.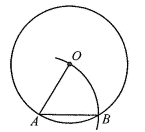 13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).14. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长,进而确定圆周率.某圆的半径为R,其内接正十二边形的周长为C.若R= , 则C= , ≈(结果精确到0.01,参考数据:≈2.449,≈1.414).14. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .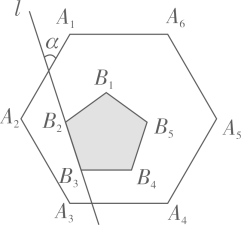
三、解答题