广东省潮州市2022届高三上学期数学期末考试试卷

试卷更新日期：2022-01-25 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {0 ， 1 ， 2}$ ， $B = {1 ， m}$ ．若 $B \subseteq A$ ，则m等于（）

A、0 B、0或1 C、0或2 D、1或2

查看试题解析
2. 已知i为虚数单位，复数 $z = \frac{1 - i^{2}}{1 + i}$ ，则z的虚部为（）

A、0 B、－1 C、－i D、1

查看试题解析
3. 等差数列 ${a_{n}}$ 的前n项和 $S_{n}$ ，若 $S_{19} = 19 ，则 a_{3} + a_{17}$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 已知 $c o s x = \frac{1}{3} ，$ 则 $s i n (\frac{π}{2} + 2 x) =$ （）

A、 $- \frac{7}{9}$ B、 $\frac{7}{9}$ C、 $- \frac{8}{9}$ D、 $\frac{8}{9}$

查看试题解析
5. 若一个圆锥的侧面积是底面面积的2倍，则该圆锥的母线与其底面所成的角的大小为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析
6. 在 $∠ A = 90 °$ 的等腰直角 $△ A B C$ 中， $E$ 为 $A B$ 的中点， $F$ 为 $B C$ 的中点， $\vec{B C} = λ \vec{A F} + μ \vec{C E}$ ，则 $λ =$ （）

A、 $- \frac{2}{3}$ B、 $- \frac{3}{2}$ C、 $- \frac{4}{3}$ D、-1

查看试题解析
7. 当前，新冠肺炎疫情进入常态化防控新阶段，防止疫情输入的任务依然繁重，疫情防控工作形势依然严峻、复杂．某地区安排A，B，C，D，E五名同志到三个地区开展防疫宣传活动，每个地区至少安排一人，且A，B两人安排在同一个地区，C，D两人不安排在同一个地区，则不同的分配方法总数为（）

A、30种 B、36种 C、42种 D、64种

查看试题解析
8. $F_{1}$ 、 $F_{2}$ 分别为双曲线 $C ： x^{2} - \frac{y^{2}}{2} = 1$ 的左、右焦点，过 $F_{1}$ 的直线 $l$ 与 $C$ 的左、右两支曲线分别交于 $A$ 、 $B$ 两点，若 $l ⊥ F_{2} B$ ，则 $\vec{F_{2} A} \cdot \vec{F_{2} B} =$ （）

A、 $4 - 2 \sqrt{3}$ B、 $4 + \sqrt{3}$ C、 $6 - 2 \sqrt{5}$ D、 $6 + 2 \sqrt{5}$

查看试题解析

二、多选题

9. 千百年来，我国劳动人民在生产实践中根据云的形状、走向速度、厚度、颜色等的变化，总结了丰富的“看云识天气”的经验，并将这些经验编成谚语，如“天上钩销云，地上雨淋林”“日落云里走，雨在半夜后”……小明同学为了验证“日落云里走，雨在半夜后”，观察了所在地区A的100天日落和夜晚天气，得到如下2×2列联表：
夜晚天气
日落云里走
下雨
不下雨
临界值表
$P (K^{2} \geq k_{0})$
0.10
0.05
0.010
0.001
出现
25
5
不出现
25
45
$k_{0}$
2.706
3.841
6.635
10.828
并计算得到 $K^{2} = 19.05$ ，下列小明对地区 $A$ 天气判断正确的是（）

A、夜晚下雨的概率约为 $\frac{1}{5}$ B、未出现“日落云里走”，但夜晚下雨的概率约为 $\frac{5}{14}$ C、出现“日落云里走”，有 $99.9 %$ 的把握认为夜晚会下雨 D、有 $99.9 %$ 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关

查看试题解析
10. 已知实数 $a ， b ， c$ 满足 $a > 1 > b > c > 0$ ，则下列说法正确的是（）

A、 $a^{a} > b^{b}$ B、 $l o g_{c} a < l o g_{b} a$ C、 $l o g_{c} a < a^{c}$ D、 $b^{\frac{1}{2}} < c^{\frac{1}{2}}$

查看试题解析
11. 已知抛物线C： $x^{2} = 2 p y (p > 0)$ ，过其准线上的点T(1，-1)作C的两条切线，切点分别为A、B，下列说法正确的是（）

A、p=1 B、抛物线的焦点为F(0，1) C、 $T A ⊥ T B$ D、直线AB的斜率为 $\frac{1}{2}$

查看试题解析
12. 已知函数 $f (x) = s i n^{n} x + c o s^{n} x (n \in N *)$ ，则（）

A、对任意正奇数n，f(x)为奇函数 B、当n=3时，f(x)在[0， $\frac{π}{2}$ ]上的最小值为 $\frac{\sqrt{2}}{2}$ C、当n=4时，f(x)的单调递增区间是 $[- \frac{π}{4} + k π ， k π] (k \in Z)$ D、对任意正整数n，f(x)的图象都关于直线 $x = \frac{π}{4}$ 对称

查看试题解析

三、填空题

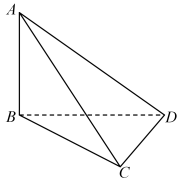
13. 设 ${a_{n}}$ 是首项为2的等比数列， $S_{n}$ 是其前n项和．若 $a_{1} + a_{2} a_{3} = 34$ ，则 $S_{5} =$ ．

查看试题解析
14. $(x^{2} + \frac{1}{x})^{6}$ 的展开式中常数项是．

查看试题解析
15. 曲线 $y = \ln x + a x$ 与直线 $y = 2 x - 1$ 相切，则 $a =$ ．

查看试题解析
16. 在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A-BCD中，AB $⊥$ 平面BCD，CD $⊥$ AD，AB=BD= $\sqrt{2}$ ，已知动点E从C点出发，沿外表面经过棱AD上一点到点B的最短距离为 $\sqrt{10}$ ，则该棱锥的外接球的表面积为．

查看试题解析

四、解答题

17. 设等差数列 ${a_{n}}$ 的前n项和为 $S_{n} ， a_{3} = 6 ， a_{7} = 14$ ．

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ 及前n项和 $S_{n}$ ；

(2)、若_________，求数列 ${b_{n}}$ 的前n项和 $T_{n}$ ．
在 $① b_{n} = 2^{a_{n}} a_{n} ； ② b_{n} = \frac{a_{n}^{2} + a_{n + 1}^{2}}{S_{n}} ；$ 这两个条件中任选一个补充在第（2）问中，并求解．

(注意：如果选择多个条件分别解答，按第一个解答计分)

查看试题解析
18. 如图所示，在四棱锥P-ABCD中，AB//CD， $A D = A B = \frac{1}{2} C D = 2$ ， $∠ D A B = 6 0^{°}$ ，点E，F分别为CD，AP的中点．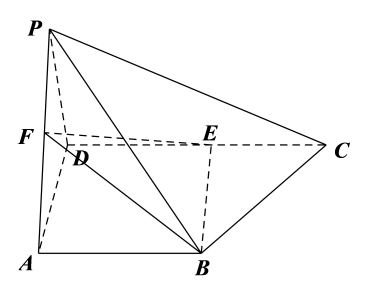

(1)、证明：PC//平面BEF；

(2)、若PA $⊥$ PD，且PA=PD，面PAD $⊥$ 面ABCD，求二面角C-BE-F的余弦值．

查看试题解析
19. 甲、乙两所学校之间进行排球比赛，采用五局三胜制(先赢3局的学校获胜，比赛结束)，约定比赛规则如下：先进行男生排球比赛，共比赛两局，后进行女生排球比赛，直到分出胜负．按照以往比赛经验，在男生排球比赛中，每局甲校获胜的概率为 $\frac{2}{3}$ ，乙校获胜的概率为 $\frac{1}{3}$ ，在女生排球比赛中，每局甲校获胜的概率为 $\frac{1}{3}$ ，乙校获胜的概率为 $\frac{2}{3}$ ，每局比赛结果相互独立．

(1)、求甲校以3：1获胜的概率；

(2)、记比赛结束时女生比赛的局数为 $ξ$ ，求 $ξ$ 的分布列及期望．

查看试题解析
20. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c， $b c o s C = a + \frac{\sqrt{3}}{3} c s i n B$ ，

(1)、求角B的大小；

(2)、若点D在边AC上，且AD=2DC，BD=2，求 $△ A B C$ 面积的最大值．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{6}}{3}$ ，以原点O为圆心，椭圆C的长半轴长为半径的圆与直线 $2 x - \sqrt{2} y + 6 = 0$ 相切．

(1)、求椭圆C的标准方程；

(2)、已知点A，B为动直线y=k(x-2)(k≠0)与椭圆C的两个交点，问：在x轴上是否存在定点E，使得 $\vec{E A^{2}} + \vec{E A} \cdot \vec{A B}$ 为定值？若存在，试求出点E的坐标和定值；若不存在，请说明理由．

查看试题解析
22. 已知函数 $f (x) = \frac{x^{2}}{2} + (a - 3) x + a l n x (a \in R)$ ，在定义域上有两个极值点 $x_{1} ， x_{2} ，且 x_{1} < x_{2}$ ．

(1)、求实数a的取值范围；

(2)、求证： $f (x_{1}) + f (x_{2}) + 5 > 0$

查看试题解析

夜晚天气日落云里走	下雨	不下雨	临界值表
			$P (K^{2} \geq k_{0})$	0.10	0.05	0.010	0.001
出现	25	5
不出现	25	45	$k_{0}$	2.706	3.841	6.635	10.828