27.3 圆中的计算问题----华师大版九年级下册同步试卷

试卷更新日期：2022-01-25 类型：同步测试

进入出卷网下载

一、单选题

1. 已知圆心角度数为60°，半径为30，则这个圆心角所对的弧长为（　　）

A、20π B、15π C、10π D、5π

查看试题解析
2. 已知扇形的半径为6，圆心角为10°，则扇形的面积为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、π D、2π

查看试题解析
3. 三个正方形方格在扇形中的位置如图所示，点O为扇形的圆心，格点A，B，C分别在扇形的两条半径和弧上，已知每个方格的边长为1，则 $\overset{⌢}{E F}$ 的长为（）

A、 $π c m$ B、 $\frac{\sqrt{10}}{4} π c m$ C、 $\frac{\sqrt{10}}{2} π c m$ D、 $2 π c m$

查看试题解析
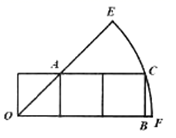4. 如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（）

A、3π B、 $\frac{3 π}{2}$ C、6π D、24π

查看试题解析
5. 一个形如圆锥冰淇淋纸筒，其底面直径为6cm，母线长为10cm，围成这样的冰淇淋纸筒所需纸的面积是（）

A、60πcm² B、15πcm² C、28πcm² D、30πcm²

查看试题解析
6. 如图，在等腰△ABC中，∠BAC＝120°，AD是∠BAC的角平分线，且AD＝6，以点A为圆心，AD长为半径画弧 $\overset{⌢}{E F}$ ，交AB于点E，交AC于点F，将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高为（　　）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{2}$

查看试题解析
7. 如图是一个几何体的三视图，根据图中所标数据计算这个几何体的体积为（）

A、 $12 π$ B、 $18 π$ C、 $24 π$ D、 $30 π$

查看试题解析
8. 一个圆柱体和一个圆锥体的底面周长之比是 $1 ： 3$ ，它们的体积比也是 $1 ： 3$ ，圆柱和圆锥的高的比是（）

A、1：1 B、3：1 C、1：9 D、1：3

查看试题解析
9. 如图，一圆柱体的底面周长为3πcm，高AB为4cm，BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，爬行的最短路程是（）.

A、3πcm B、5cm C、 $\sqrt{9 π^{2} + 16}$ cm D、 $\sqrt{2.25 π^{2} + 16}$ cm

查看试题解析
10. 如图，⊙O的直径AB＝5，弦AC＝3，点D是劣弧BC上的动点，CE⊥DC交AD于点E，则OE的最小值是（）

A、 $\frac{5}{4}$ B、 $\frac{2 - \sqrt{2}}{3}$ C、2－ $\sqrt{2}$ D、 $\sqrt{2}$ －1

查看试题解析

二、填空题

11. 已知弧的长是 $\frac{5}{3}$ π，弧的半径为3，则该弧所对的圆心角度数为°.

查看试题解析
12. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为150°，AB的长为18cm，则弧BC的长为cm．

查看试题解析
13. 一个扇形的圆心角为 $100 °$ ，面积为 $15 π c m^{2}$ ，则此扇形的半径长为cm.

查看试题解析
14. 如图，圆锥的轴截面（过圆锥顶点和底面圆心的截面）是边长为4cm的等边三角形 $A B C$ ，点D是母线 $A C$ 的中点，一只蚂蚁从点B出发沿圆锥的表面爬行到点D处，则这只蚂蚁爬行的最短距离是cm．

查看试题解析
15. 有一个不完整圆柱形玻璃密封容器如图①，测得其底面半径为a ，高为h ，其内装蓝色液体若干．若如图②放置时，测得液面高为 $\frac{1}{2} h$ ；若如图③放置时，测得液面高为 $\frac{2}{3} h .$ 则该玻璃密封容器的容积 $($ 圆柱体容积 $=$ 底面积 $\times$ 高 $)$ 是．（结果保留 $π$ ）

查看试题解析
16. 如图所示，AB是⊙O的直径，AD、BC是⊙O的两条切线，E、F分别在AD、BC上，EF切⊙O于点G，连接OE、OF、BG、AG，BG与OF相交于点M，AG与OE相交于点N，已知AE＝2，BF＝8．以下结论：①⊙O的半径为2；②AG∥OF；③BG＝ $\frac{16 \sqrt{5}}{5}$ ；④四边形OMGN是正方形．其中正确的结论有（填序号）．

查看试题解析

三、解答题

17. 如图，在△ABC中，AB＝AC＝8cm，∠BAC＝40°，以腰AB为直径作半圆O，分别交BC，AC于点D，E．求 $\overset{⌢}{B D}$ ， $\overset{⌢}{A E}$ 的长．

查看试题解析
18. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径r=2 cm，扇形的圆心角θ=120°，求该圆锥的高h的长.

查看试题解析

四、综合题

19. 已知， $△ A B C$ 内接于 $⊙ O$ ，AD、BD为 $⊙ O$ 的弦，且 $∠ A C B + 2 ∠ A B D = 180 °$ ．

(1)、如图1，求证： $A D = B D$ ；

(2)、如图2，过B作 $⊙ O$ 的切线交AC的延长线于E，求证： $∠ A B D = ∠ E B D$ ；

(3)、如图3，在（2）的条件下，连接CD，若 $∠ E = 2 ∠ D B C$ ， $B D = 3 C D$ ， $B E = 6$ ，求CE的长度．

查看试题解析