四川省南充市2021-2022学年高二上学期理数期末考试试卷

试卷更新日期：2022-01-25 类型：期末考试

进入出卷网下载

一、单选题

1. 直线 $x - \sqrt{3} y + 3 = 0$ 的倾斜角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
2. 采用简单随机抽样的方法，从含有6个个体的总体中抽取1个容量为3的样本，某个个体被抽到的概率是（）.

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{5}$

查看试题解析
3. 不等式组 ${\begin{array}{l} x - y + 1 < 0 \\ x + y - 3 \geq 0 \end{array}$ 表示的区域（阴影部分）是（）

A、 B、 C、 D、

查看试题解析
4. 已知直线 $l ： y = k x + b$ ，则“ $b > 0$ ”是“直线 $l$ 过第一､二象限”的（）条件

A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要

查看试题解析
5. 已知命题 $p ： \exists x_{0} \in (0 ， + \infty) ， 3 x_{0} > x_{0}^{3}$ ，则 $\neg p$ 是（）

A、 $\exists x_{0} \in (- \infty ， 0] ， 3 x_{0} \leq x_{0}^{3}$ B、 $\exists x_{0} \in (- \infty ， 0] ， 3 x_{0} > x_{0}^{3}$ C、 $\forall x \in (0 ， + \infty) ， 3 x > x^{3}$ D、 $\forall x \in (0 ， + \infty) ， 3 x \leq x^{3}$

查看试题解析
6. 青少年视力被社会普遍关注，为了解他们的视力状况，经统计得到图中右下角12名青少年的视力测量值 $a_{i} (i = 1 ， 2 ， 3 ， \cdot \cdot \cdot ， 12)$ （五分记录法）的茎叶图，其中茎表示个位数，叶表示十分位数．如果执行如图所示的算法程序，那么输出的结果是（）

A、4 B、5 C、6 D、7

查看试题解析
7. 已知点 $P (m ， n)$ 在圆 $O ： x^{2} + y^{2} = 1$ 内部，则直线 $m x + n y = 1$ 与圆 $O$ 的公共点有（）

A、0个 B、1个 C、2个 D、1或2个

查看试题解析
8. 一人打靶中连续射击两次，事件“至少有一次中靶”的互斥事件是（）

A、至多有一次中靶 B、两次都中靶 C、两次都不中靶 D、只有一次中靶

查看试题解析
9. 设 $f (x ， y) = \sqrt{x^{2} + y^{2}} + \sqrt{(x + 2)^{2} + y^{2}} + \sqrt{(2 - x)^{2} + (y + 3)^{2}} + \sqrt{x^{2} + (y + 4)^{2}}$ ，其中 $- 2 \leq x \leq 2 ， - 4 \leq y \leq 0$ .则 $f (x ， y)$ 的最小值为（）

A、8 B、9 C、 $6 + \sqrt{13}$ D、 $4 + 3 \sqrt{5}$

查看试题解析
10. 过定点M的直线 $a x + y - 1 = 0$ 与过定点N的直线 $x - a y + 3 a - 2 = 0$ 交于点P，则 $| \vec{P M} | + | \vec{P N} |$ 的最大值为（）

A、2 B、 $2 \sqrt{2}$ C、4 D、8

查看试题解析
11. 已知圆 $C_{1} ： x^{2} + y^{2} - 2 x + 4 y + 4 = 0$ ，圆 $C_{2} ： x^{2} + y^{2} + x - y - m^{2} = 0 (m > 0)$ ，若圆 $C_{2}$ 平分圆 $C_{1}$ 的圆周，则正数 $m$ 的值为（）

A、3 B、2 C、4 D、1

查看试题解析
12. 已知P是圆 $C ： (x - 1)^{2} + (y - 2)^{2} = 1$ 外一动点，过点P作圆C的切线，切点分别为A、B，总有 $△ P A B$ 为正三角形．当点P运动时，直线 $l ： 3 x - 4 y - 10 = 0$ 上存在两点M、N，使得 $\vec{P M} \cdot \vec{P N} \leq 0$ 恒成立，则线段 $M N$ 长度的最小值是（）

A、10 B、8 C、5 D、2

查看试题解析

二、填空题

13. 在空间直角坐标系中，点 $A (1 ， - 2 ， 3)$ 关于面 $x O z$ 的对称点为B，则线段 $A B$ 的长度为．

查看试题解析
14. 将某班的60名学生编号为 $01 ， 02 ， \dots ， 60$ ，采用系统抽样方法抽取一个容量为5的样本，且随机抽得的第一个号码为03，则抽得的最大号码是.

查看试题解析
15. 已知直线 $x - \sqrt{3} y + 3 = 0$ 与直线 $2 x - a y + 2 = 0$ 平行，则这两直线之间的距离为.

查看试题解析
16. 太极图被称为“中华第一图”，其形状如阴阳两鱼互纠在一起，展现了一种相互转化、相对统一的和谐美，闪烁着中华文明进程的光辉．在某个太极图图案中，阴影部分可用集合 $A = {(x ， y) | x^{2} + {(y - 1)}^{2} \leq 1 或 {\begin{array}{l} x^{2} + y^{2} \leq 4 \\ x^{2} + {(y + 1)}^{2} \geq 1 \\ x \leq 0 \end{array}}$ 表示．设点 $(x ， y) \in A$ ，则 $Z = \frac{3 x + y - 10}{x - 3}$ 的最大值和最小值之积为．

查看试题解析

三、解答题

17. 已知命题 $p ： \forall x \in [- 1 ， 3]$ ，都有 $m \geq x$ 成立；命题 $q ： \exists x_{0} \in [- 1 ， 3]$ ，使 $m \geq x_{0}$ 成立.若 $(\neg p) \land q$ 为真命题，求实数 $m$ 的取值范围.

查看试题解析
18. 某省电视台为了了解该省卫视一档成语类节目的收视情况，抽查东、西部各5个城市，得到观看节目的人数的统计数据（单位：千人），并画出如下的茎叶图，其中西部人数一个数字被污损，用m表示（ $m \in N$ ）．
附：参考公式： $b = \frac{\sum_{i = 1} (x_{i} - x) (y_{i} - y)}{\sum_{i = 1} {(_{x} - x)}^{2}} = \frac{\sum_{i = 1} x_{i} y_{i} - n \bar{x y}}{\sum_{i = 1} x_{i}^{2} - n x^{2}} ，  a = y - b x$

(1)、若东部各城市观看该节目的观众的中位数不超过西部各城市观看该节目的观众的平均人数，求m的值；

(2)、该节目的播出极大地激发了观众对成语知识学习积累的热情，现从观看节日的观众中随机统计了4位观众周均学习成语知识的时间y（单位：小时）与年龄x（单位：岁），并制作了如下对照表：
年龄x（岁）
20
30
40
50
周均学习成语知识时间y（小时）
2.5
3
4
4.5
根据表中数据，用最小二乘法原理求出周均学习成语知识的时间y与年龄x的线性回归方程 $y = b x + a$ ，并预测年龄为60岁的观众周均学习成语知识的时间．

查看试题解析
19. 已知 $△ A B C$ 中，顶点 $A (0 ， 6) ， B (12 ， 2) ， ∠ A C B$ 的平分线所在直线的方程为 $x - y = 0$ .

(1)、求BC边所在的直线方程；

(2)、求 $△ A B C$ 的内切圆方程.

查看试题解析
20. 某校在2021年的综合素质冬令营初试成绩中随机抽取40名学生的笔试成绩，并将成绩共分成五组：第1组 $[75 ， 80)$ ，第2组 $[80 ， 85)$ ，第3组 $[85 ， 90)$ ，第4组 $[90 ， 95)$ ，第5组 $[95 ， 100]$ ，得到的频率分布直方图如图所示．且同时规定成绩小于85分的学生为“良好”，成绩在85分及以上的学生为“优秀”，且只有成绩为“优秀”的学生才能获得面试资格，面试通过者将进入复试．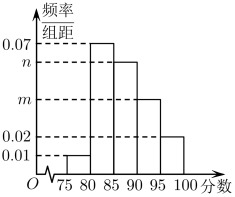

(1)、根据样本频率分布直方图估计样本的众数；

(2)、如果用分层抽样的方法从“良好”和“优秀”的学生中共选出5人，再从这5人中选2人发言，那么这两人中至少有一人是“优秀”的概率是多少？

(3)、如果第三、四、五组的人数成等差数列，规定初试时笔试成绩得分从高到低排名在前18%的学生可直接进入复试，根据频率分布直方图估计初试时笔试成绩至少得到多少分才能直接进入复试？

查看试题解析
21. 已知圆 $Q ： (x - 5)^{2} + y^{2} = 1$ 和点 $M (10 ， 0)$ ，直线 $l ： y = 2 x + 5$ ．

(1)、点A在圆Q上运动，且A为线段 $M N$ 的中点，求点N的轨迹曲线T的方程；

(2)、点P是直线l上的动点，过P作（1）中曲线T的两条切线 $P B$ 、 $P C$ ，切点为B，C，求直线 $B C$ 所过定点D的坐标；

(3)、设E为（1）中曲线T上任意一点，过点E向圆Q引一条切线，切点为F．试探究：x轴上是否存在定点G（异于点Q），使得 $\frac{| E F |^{2} + 1}{| E G |^{2}}$ 为定值？若存在，求 $\frac{2}{5} | E Q | + | E F |$ 的最小值；若不存在，请说明理由．

查看试题解析
22. 已知x，y满足 $0 \leq x \leq 2 ， 0 \leq y \leq 3$ .

(1)、若 $x ， y \in N$ ，求 $x + y < 2$ 的概率；

(2)、若 $x ， y \in R$ ，求 $x + y < 2$ 的概率.

查看试题解析
23. 某广告公司接到幸福社区制作疫情防控宣传标牌的任务，要制作文字标牌4个，绘画标牌5个，该公司现有两种规格的原料，甲种规格原料每张3m² ，可做文字标牌1个和绘画标牌2个；乙种规格原料每张2m² ，可做文字标牌2个和绘画标牌1个.问两种规格的原料各用多少张时，才能使总的用料面积最小?并求最小用料面积.

查看试题解析

年龄x（岁）	20	30	40	50
周均学习成语知识时间y（小时）	2.5	3	4	4.5