上海市金山区2021-2022学年高二上学期数学期末考试试卷

试卷更新日期：2022-01-25 类型：期末考试

进入 出卷网 下载

一、填空题

  • 1. 必然事件的概率是.

    查看试题解析

  • 2. 半径为1的球的体积为 ．

    查看试题解析

  • 3. 已知向量a=(2 ， 1 ， 3) ， 向量 b=(4 ， m ， 6) ， 若a//b ， 则实数m的值为.

    查看试题解析

  • 4. 教育部门对某校学生的阅读素养进行调研，在该校随机抽取了100 名学生进 行百分制检测，现将所得的成绩按照 [40 ， 50) ， [50 ， 60) ， [60 ， 70) ， [70 ， 80) ， [80 ， 90) ， [90 ， 100]分成 6 组，并根据所得数据作出了频率分布直方图 (如图所示)，则成绩在[70 ， 80)这组的学生人数是.

    查看试题解析

  • 5. 在空间直角坐标系O−xyz 中，已知向量a=(1 ， 0 ， 3) ， 则a 在x轴上的投影向量为.

    查看试题解析

  • 6. 将边长为2 的正方形ABCD 绕其一边AB所在的直线旋转一周，所得的圆柱体积为.

    查看试题解析

  • 7. 生活中有这样的经验：三脚架在不平的地面上也可以稳固地支撑一部照相机.这个经验用我们所学的数学公理可以表述为.

    查看试题解析

  • 8. 有一组数据x1、x2、⋯ ， xn ， 其平均数为3 ，方差为2，则新的数据 x1−1 ， x2−1 ， ⋯ ， xn−1的方差为.

    查看试题解析

  • 9. 一道数学难题，在半小时内，甲能解决的概率是12 ， 乙能解决的概率是13 ， 两人试图独立地在半小时内解决它，则问题得到解决的概率是.

    查看试题解析

  • 10. 某甲､乙两人练习跳绳，每人练习10组，每组不间断跳绳计数的茎叶图如图，则下面结论中所有正确的序号是.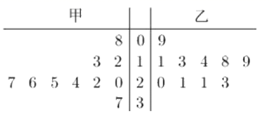

    ①甲比乙的极差大；②乙的中位数是18；③甲的平均数比乙的大；④乙的众数是21.

    查看试题解析

  • 11. 如图，四个棱长为1的正方体排成一个正四棱柱，AB是一条侧棱，Pi(i=1 ， 2 ， ⋯ ， 8)是上底面上其余的八个点，则集合{y|y=AB⇀⋅APi⇀ ， i=1 ， 2 ， 3 ， ⋯ ， 8}中的元素个数为 ．

    查看试题解析

  • 12. 我国南北朝时期的数学家祖暅提出了一个原理“幂势既同，则积不容异”，即夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截， 如果截得的两个截面的面积总相等，那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件，若该圆锥的侧面展开图是一个半径为2的半圆，则该几何体的体积为.

    查看试题解析

二、单选题

  • 13. 某家大型超市近10天的日客流量（单位：千人次）分别为：3.4、3.6、5.6、1.8、3.7、4.0、2.5、2.8、4.4、3.6.下列图形中不利于描述这些数据的是（    ）
    A、散点图 B、条形图 C、茎叶图 D、扇形图

    查看试题解析

  • 14. 设 α,β 是两个不同的平面，l是一条直线，以下命题正确的是（    ）
    A、若 l⊥α,α⊥β ，则 l⊂β B、若 l//α,α//β ，则 l⊂β C、若 l⊥α,α//β ，则 l⊥β D、若 l//α,α⊥β ，则 l⊥β

    查看试题解析

  • 15. 由小到大排列的一组数据：x1、x2、x3、x4、x5 ， 其中每个数据都小于−2 ， 另一组数据2、−x1、x2、x3、−x4、x5的中位数可以表示为（    ）
    A、x2+x32 B、x2−x12 C、2+x52 D、x3−x42

    查看试题解析

  • 16. 概率论起源于赌博问题．法国著名数学家布莱尔⋅帕斯卡遇到两个赌徒向他提出的赌金分配问题：甲、乙两赌徒约定先赢满5局者，可获得全部赌金700法郎，当甲赢了4局，乙赢了3局，不再赌下去时，赌金如何分配？假设每局两人输赢的概率各占一半，每局输赢相互独立，那么赌金分配比较合理的是（    ）
    A、甲525法郎，乙175法郎 B、甲500法郎，乙200法郎 C、甲400法郎，乙300法郎 D、甲350法郎，乙350法郎

    查看试题解析

三、解答题

  • 17. 同时抛掷两颗骰子，观察向上的点数.
    (1)、试表示 “出现两个1点”这个事件相应的样本空间的子集；
    (2)、求出现两个1点”的概率；
    (3)、求“点数之和为7”的概率.

    查看试题解析

  • 18. 如图，已知正方体ABCD−A1B1C1D1的棱长为4 ， P ， Q分别是棱BC与B1C1的中点.

    (1)、求以A1 ， D1 ， P ， Q为顶点的四面体的体积；
    (2)、求异面直线D1P和A1Q所成的角的大小.

    查看试题解析

  • 19. 如图，在正方体ABCD−A1B1C1D1中，E是棱DD1的中点.

    (1)、试判断直线BD1与平面AEC的位置关系，并说明理由；
    (2)、求证：直线BD1⊥面AB1C.

    查看试题解析

  • 20. 如图，在直棱柱ABC−A1B1C1 中，已知AA1=AB=AC=2 ， AB⊥AC ， 点D、E、F分别A1B1、CC1、BC的中点.

    (1)、求异面直线AE与DF所成的角的大小；
    (2)、求点A到平面DEF的距离；
    (3)、在棱AA1上是否存在一点M ， 使得直线ME与平面DEF所成的角的大小是45∘? 若存在，请指出点M的位置，若不存在，请说明理由.

    查看试题解析

  • 21. 如图，P−ABC是底面边长为1的正三棱锥，D ， E ， F分别为棱PA ， PB ， PC上的点，截面DEF//底面ABC ， 且棱台DEF−ABC与棱锥P−ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

    (1)、求证：P−ABC为正四面体；
    (2)、若PD=12PA ， 求二面角D−BC−A的大小；
    (3)、设棱台DEF−ABC的体积为V ， 是否存在体积为V且各棱长均相等的直四棱柱，使得它与棱台DEF−ABC有相同的棱长和? 若存在，请具体构造出这样的一个直四棱柱，并给出证明；若不存在，请说明理由.

    查看试题解析