湖南省长沙市长沙县、望城区、浏阳市2021-2022学年高二上学期数学期末调研考试试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 若两直线 与 平行,则 的值为( )A、±2 B、2 C、-2 D、02. 若抛物线 过点 ,则该抛物线的焦点坐标为( )A、 B、 C、 D、3. 若曲线 在 处的切线,也是 的切线,则 ( )A、-1 B、1 C、2 D、e4. 在平面直角坐标系中,椭圆的中心在原点,焦点在轴上,离心率为 , 过的直线交椭圆于两点,且的周长为16,则椭圆的方程为( )A、 B、 C、 D、5. 在等比数列中,是函数的极值点,则( )A、-4 B、-3 C、3 D、46. 已知过点的直线与圆相切,且与直线垂直,则( )A、 B、 C、-2 D、27. 已知矩形 , 为平面 外一点,且 平面 , , 分别为 , 上的点,且 , , ,则 ( )
 A、 B、 C、1 D、8. 已知函数是定义在上的奇函数,是的导函数,且 , 当时 , 则使得成立的的取值范围是( )A、 B、 C、 D、
A、 B、 C、1 D、8. 已知函数是定义在上的奇函数,是的导函数,且 , 当时 , 则使得成立的的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知双曲线 过点 且渐近线为 ,点 在双曲线 的一条渐近线上, 为坐标原点, 为双曲线的右焦点,则下列结论正确的是( )A、双曲线 的离心率为2 B、双曲线 的方程是 C、 的最小值为2 D、直线 与 有两个公共点10. 已知递减的等差数列 的前 项和为 , ,则( )A、 B、 最大 C、 D、11. 下列说法错误的是( )A、若直线 与直线 互相垂直,则 B、直线 的倾斜角 的取值范围是 C、过 , 两点的所有直线的方程为 D、经过点 且在 轴和 轴上截距都相等的直线方程为12. 已知函数 , 若区间的最小值为-1且最大值为1,则的值可以是( )A、0 B、4 C、 D、
三、填空题
-
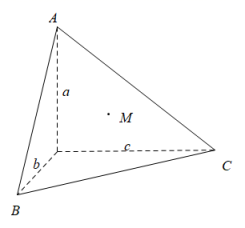
13. 九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜,据明代杨慎《丹铅总录》记载:“两环互相贯为一,得其关捩,解之为二,又合面为一”,在某种玩法中,用表示解下个圆环所需的移动最少次数,若 , 且 , 则解下5个环所需的最少移动次数为.14. 已知函数在上是单调递增函数,则实数的取值范围是.15. 如图,在三棱锥中,三条侧棱OA,OB,OC两两垂直,且OA,OB,OC的长分别为a,b,c,M为内部及其边界上的任意一点,点M到平面OBC,平面OAC,平面OAB的距离分别为 , , , 则.
 16. 我们通常称离心率为的椭圆为“黄金椭圆”.如图,已知椭圆 , A1 , A2分别为左、右顶点,B1 , B2分别为上、下顶点,F1 , F2分别为左、右焦点,P为椭圆上一点,现给出以下四个条件:①;②;③轴,且;④四边形的的内切圆过焦点 , .其中能使椭圆C为“黄金椭圆”的条件是和.
16. 我们通常称离心率为的椭圆为“黄金椭圆”.如图,已知椭圆 , A1 , A2分别为左、右顶点,B1 , B2分别为上、下顶点,F1 , F2分别为左、右焦点,P为椭圆上一点,现给出以下四个条件:①;②;③轴,且;④四边形的的内切圆过焦点 , .其中能使椭圆C为“黄金椭圆”的条件是和.
四、解答题
-
17. 解答下列各题:(1)、求两条平行直线与间的距离.(2)、求曲线在点处的切线方程.18. 已知数列的前n项和为 , 且(),.数列为等比数列,且.
(Ⅰ)求和的通项公式;
(Ⅱ)设 , 求数列的前项和.
19. 如图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度AB=20 m,拱高OP=4 m,建造时每间隔4 m需要用一根支柱支撑,求支柱A2P2的高度.(结果保留两位小数)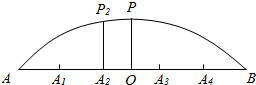 20. 在如图所示的多面体中,且. , 且 , 且 , 平面ABCD,.
20. 在如图所示的多面体中,且. , 且 , 且 , 平面ABCD,. (1)、求点F到直线EC的距离;(2)、求平面BED与平面EDC夹角的余弦值.
(1)、求点F到直线EC的距离;(2)、求平面BED与平面EDC夹角的余弦值.
