27.2.1 点与圆的位置关系----华师大版九年级下册同步试卷

试卷更新日期：2022-01-25 类型：同步测试

进入出卷网下载

一、单选题

1. 已知⊙O的半径为5，点P在⊙O外，则OP的长可能是（）。

A、3 B、4 C、5 D、6

查看试题解析
2. 已知⊙O的半径为3，点P到圆心O的距离为4，则点P（）

A、在⊙O内 B、在⊙O上 C、在⊙O外 D、无法确定

查看试题解析
3. 同一平面内，一个点到圆的最小距离为 $6 cm$ ，最大距离为 $8 cm$ ，则该圆的半径为（）

A、 $7 cm$ 或 $14 cm$ B、 $2 cm$ 或 $14 cm$ C、 $1 cm$ 或 $7 cm$ D、 $1 cm$ 或 $6 cm$

查看试题解析
4. 下列命题中，正确的命题是（）

A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定重直于弦 D、相等的两个圆心角所对的两条弧相等

查看试题解析
5. 如图，由边长为1的正方形组成的6×5网格中，一块含45°的三角板ABC的斜边AB始终经过格点N，AC始终经过格点M，点A在MN下方运动，格点P到A的距离最小值为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{13}$ ﹣1 D、2 $\sqrt{2}$ ﹣2

查看试题解析
6. 已知矩形ABCD的边AB=15，BC=20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是（）.

A、r＞15 B、15＜r＜20 C、15＜r＜25 D、20＜r＜25

查看试题解析
7. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内， $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $O$ 均是正六边形的顶点.则点 $O$ 是下列哪个三角形的外心（）.

A、 $△ A E D$ B、 $△ A B D$ C、 $△ B C D$ D、 $△ A C D$

查看试题解析
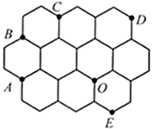8. 引理：在 $△ A B C$ 中，若 $D$ 为 $B C$ 的中点，则 $A B^{2} + A C^{2} = 2 A D^{2} + 2 C D^{2}$ .（中线长公式，不用证明，可以直接应用）根据这个引理，解决下面的问题：如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，点 $P$ 在以 $B C$ 为直径的半圆上运动，则 $P A^{2} + P D^{2}$ 的最小值是（）

A、 $2 \sqrt{10}$ B、38 C、40 D、68

查看试题解析

二、填空题

9. 已知⊙O的半径为3，且点A到圆心的距离是5，则点A与⊙的位置关系是 .

查看试题解析
10. ⊙O内一点P到⊙O上的最近点的距离为2，最远点的距离为4，则⊙O的半径为 .

查看试题解析
11. 如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为.

查看试题解析
12. 如图，O是 $△ A B C$ 的外心，且∠ABC=40°，∠ACB=70°，则 $∠ B O C =$ ．

查看试题解析
13. 已知以AB为直径的圆O，C为AB弧的中点，P为BC弧上任意一点， CD⊥CP交AP于D，连结BD，若AB=6，则BD的最小值为 .

查看试题解析

三、解答题

14. 已知⊙O的半径为2，点P到圆心O的距离OP=m，且m使关于x的方程 $2 x^{2} - 2 \sqrt{2} x + m - 1 = 0$ 有实数根，求点P与⊙O的位置关系.

查看试题解析
15. 如图，AB、AC是⊙O的两条弦，且AB=AC．求证：∠1=∠2．

查看试题解析
16.
（1）已知⊙O的直径为10cm，点A为⊙O外一定点，OA=12cm，点P为⊙O上一动点，求PA的最大值和最小值．
（2）如图：= ， D、E分别是半径OA和OB的中点．求证：CD=CE．

查看试题解析