27.1 圆的认识----华师大版九年级下册同步试卷
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 下列图形中, 为圆心角的是( )A、
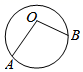 B、
B、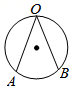 C、
C、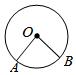 D、
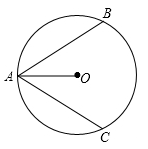
D、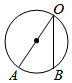 2. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )
2. 如图,以AB为直径的半圆上有一点C,∠C=25°,则 的度数为( )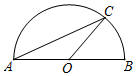 A、25° B、30° C、50° D、65°3. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( )
A、25° B、30° C、50° D、65°3. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为10cm,AB=16cm,则CD的长是( ) A、2cm B、3cm C、4cm D、5cm4. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
A、2cm B、3cm C、4cm D、5cm4. 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )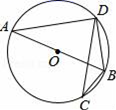 A、116° B、32° C、58° D、64°5. 如图,是的直径,C、D是上两点, , 则等于( )
A、116° B、32° C、58° D、64°5. 如图,是的直径,C、D是上两点, , 则等于( ) A、 B、 C、 D、6. 如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( )
A、 B、 C、 D、6. 如图,四个边长为2的小正方形拼成一个大正方形,A、B、O是小正方形顶点,⊙O的半径为2,P是⊙O上的点,且位于右上方的小正方形内,则∠APB等于( ) A、30° B、45° C、60° D、90°7. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
A、30° B、45° C、60° D、90°7. 如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( ) A、 B、 C、 D、8. 如图,AB为半圆O的直径,CD= AB= ,AD,BC交于点E,且E为CB的中点,F为弧AC的中点,连接EF,则EF的长为( )
A、 B、 C、 D、8. 如图,AB为半圆O的直径,CD= AB= ,AD,BC交于点E,且E为CB的中点,F为弧AC的中点,连接EF,则EF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,已知在半径为10的⊙O中,弦AB=16,OC⊥AB,则OC的长为 .
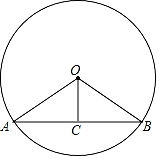 10. 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=2,则⊙O的半径为.
10. 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=2,则⊙O的半径为. 11. 如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=°.
11. 如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=°. 12. 如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为度.
12. 如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为度. 13. 如图,⊙O的直径AB垂直于弦CD,垂足为E,如果∠B=60°,AC=6,则CD的长为
13. 如图,⊙O的直径AB垂直于弦CD,垂足为E,如果∠B=60°,AC=6,则CD的长为 14. 如图是郑州圆形“戒指桥”,其数学模型为如图所示.已知桥面跨径AB=20米,D为圆上一点,DC⊥AB于点C,且CD=BC=14米,则该圆的半径长为 米.
14. 如图是郑州圆形“戒指桥”,其数学模型为如图所示.已知桥面跨径AB=20米,D为圆上一点,DC⊥AB于点C,且CD=BC=14米,则该圆的半径长为 米. 15. 如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2 m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为m.
15. 如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2 m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为m.
三、解答题