2021-2022学年浙教版数学九下2.2切线长定理同步练习
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 如图, 为 的直径,点P在 的延长线上, 与 相切,切点分别为C,D.若 ,则 等于( )
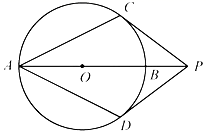 A、 B、 C、 D、2. 如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是
A、 B、 C、 D、2. 如图, 的直径AB=8,AM,BN是它的两条切线,DE与 相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,则BF的长是 A、 B、 C、 D、3. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( )
A、 B、 C、 D、3. 如图,从圆外一点 引圆的两条切线 , , , 为切点, 为 上的一点,连接 交 于点 ,若 , , ,则 的半径长是( ) A、 B、 C、 D、4. 已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )A、0 B、1 C、2 D、35. 如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A、 B、 C、 D、4. 已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )A、0 B、1 C、2 D、35. 如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( ) A、DC=DT B、AD= DT C、BD=BO D、2OC=5AC6. 如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( )
A、DC=DT B、AD= DT C、BD=BO D、2OC=5AC6. 如图AB、BC、CD分别与⊙O 相切于E、 F、G 三点且AB DC,则下列结论:①CG=CF;②BE=BF;③∠BOC=90°;④△BEO~△BOC~△OGC中正确的个数是( ) A、4 B、3 C、2 D、17. 如图, 、 、 是 的切线,切点分别是 、 、 , 分别交 、 于 、 两点,若 ,则 的度数( )
A、4 B、3 C、2 D、17. 如图, 、 、 是 的切线,切点分别是 、 、 , 分别交 、 于 、 两点,若 ,则 的度数( ) A、50° B、60° C、70° D、75°8. 如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q , 以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与 相交,那么r的取值范围是( )
A、50° B、60° C、70° D、75°8. 如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q , 以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与 相交,那么r的取值范围是( )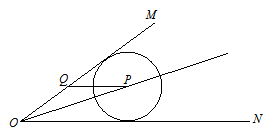 A、4<r<12 B、2<r<12 C、4<r<8 D、r>49. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A、4<r<12 B、2<r<12 C、4<r<8 D、r>49. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )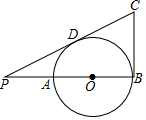 A、1.5 B、2 C、 D、10. 如图,⊙O与∠α的两边相切,若∠α=60°,则图中阴影部分的面积S关于⊙O的半径r的函数图象大致是( )
A、1.5 B、2 C、 D、10. 如图,⊙O与∠α的两边相切,若∠α=60°,则图中阴影部分的面积S关于⊙O的半径r的函数图象大致是( )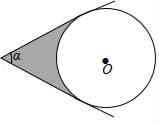 A、
A、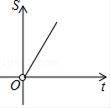 B、
B、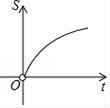 C、
C、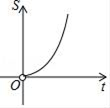 D、
D、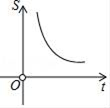
二、填空题
-
11. 如图,已知圆O为Rt△ABC的内切圆,切点分别为D、E、F,且∠C=90°,AB=13,BC=12,则圆O的半径为。
 12. 如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为.
12. 如图,在 中, ,点 为边 上一动点,连结 .以 为圆心, 为半径作圆,交 于 ,过 作⊙O的切线,交 于点 .当⊙O与边 相切时, 的长为. 13. PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为.14. 如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为.
13. PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=50°,则∠COD的度数为.14. 如图,AC与BC为⊙O的切线,切点分别为A,B,OA=2,∠ACB=60°,则阴影部分的面积为. 15. 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离.
15. 如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA,PB于点C、D,若△PCD的周长为24,⊙O的半径是5,则点P到圆心O的距离. 16. 如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为.
16. 如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为.
三、综合题
-
17. 已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
 (1)、如图①,若∠BAC=25° , 求∠AMB的大小;(2)、如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.18. 已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.
(1)、如图①,若∠BAC=25° , 求∠AMB的大小;(2)、如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.18. 已知如图:AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.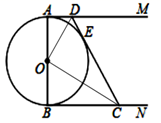 (1)、求证:(2)、求证:19. 如图,D为⊙O上一点,点C在直径BA的延长线上,CD是⊙O的切线,∠C = 30°.
(1)、求证:(2)、求证:19. 如图,D为⊙O上一点,点C在直径BA的延长线上,CD是⊙O的切线,∠C = 30°. (1)、求∠CBD的度数;(2)、过点 B 作⊙O的切线交CD的延长线于点E,若AB=6, 依题意补全图形并求DE的长.20. 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)、求∠CBD的度数;(2)、过点 B 作⊙O的切线交CD的延长线于点E,若AB=6, 依题意补全图形并求DE的长.20. 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.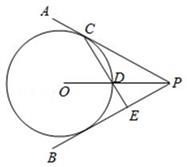 (1)、求证:PB是⊙O的切线;(2)、OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.21. 如图, 是 的切线,A为切点,点B、C、D在 上,且 .
(1)、求证:PB是⊙O的切线;(2)、OP与⊙O相交于点D,直线CD交PB于点E,若CE⊥PB,CE=4,求⊙O的半径.21. 如图, 是 的切线,A为切点,点B、C、D在 上,且 .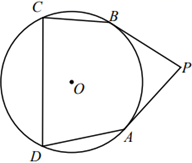 (1)、求证: 是 的切线;(2)、若 ,则 的度数为°.22. 如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .
(1)、求证: 是 的切线;(2)、若 ,则 的度数为°.22. 如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .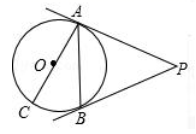 (1)、求证: 是 的切线;(2)、若 的半径为2,求弦 及 , 的长.23. 如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 .
(1)、求证: 是 的切线;(2)、若 的半径为2,求弦 及 , 的长.23. 如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 . (1)、补全图形,判断直线 与 的位置关系,并证明;(2)、若 ,求 的半径.24. 如图,射线PO与⊙O交于A、B两点,PC、PD分别与⊙O相切于点C、D.
(1)、补全图形,判断直线 与 的位置关系,并证明;(2)、若 ,求 的半径.24. 如图,射线PO与⊙O交于A、B两点,PC、PD分别与⊙O相切于点C、D. (1)、请写出两个正确结论;(2)、若PD=6,∠CPO=30°,求⊙O的半径.
(1)、请写出两个正确结论;(2)、若PD=6,∠CPO=30°,求⊙O的半径.


