第26章 二次函数----华师大版九年级下册单元试卷

试卷更新日期：2022-01-25 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 抛物线y=3(x−3)2+4顶点坐标是（    ）
    A、(−3 ， 4) B、(3 ， 4) C、(4 ， 3) D、(−4 ， 3)

    查看试题解析

  • 2. 抛物线y=-（x-1）2向右平移2个单位，平移后的抛物线的表达式为（    ）
    A、y=-（x+1）2 B、y=-（x-3）2 C、y=-（x-1）2+2 D、y=-（x-1）2-2

    查看试题解析

  • 3. 我们把“将抛物线向右平移2个单位或．向上平移1个单位”这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后得到的一条抛物线是y=x2+1，则原抛物线的表达式不可能是（ ）．
    A、y=x2－1 B、y=x2+6x+5 C、y=x2+4x+4 D、y=x2+8x+17

    查看试题解析

  • 4. 由二次函数y=−3(x+4)2−2可知（    ）
    A、其图象的开口向上 B、其顶点坐标为(4 ， 2) C、其图象的对称轴为直线x=−4 D、当x>3时，y随x的增大而增大

    查看试题解析

  • 5. 如图，小聪要在抛物线y ＝x（2-x）上找一点M（a，b），针对b的不同取值，所找点M的个数，三个同学的说法如下，

    小明：若b＝-3，则点M的个数为0；

    小云：若b ＝ 1，则点M的个数为1；

    小朵：若b ＝ 3，则点M的个数为2．

    下列判断正确的是（    ）．

    A、小云错，小朵对 B、小明，小云都错 C、小云对，小朵错 D、小明错，小朵对

    查看试题解析

  • 6. 如图，已知二次函数y=ax2+bx+c的图象与x轴交于点（-2，0）、（x1 ， 0），且1<x1 <2，与y轴交于正半轴.下列结论错误的是（           ）

     

    A、4a-2b+c=0 B、当x< −12 时，y随x增大而增大 C、当x> −12 时，y随x增大而减小 D、a<b<0

    查看试题解析

  • 7. 将二次函数y＝﹣x2＋2x＋3的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示.当直线y＝x＋b与新函数的图象恰有3个公共点时，b的值为（   ）

    A、−134 或﹣2 B、−214 或﹣2 C、−214 或﹣3 D、−134 或﹣3

    查看试题解析

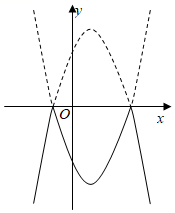  • 8. 如图，是二次函数y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：

    ①abc＜0；②b＞2a；③a+b+c=0；④8a+c＞0；⑤ax2+bx+c=0的两根分别为﹣3和1．

    其中正确的命题有（   ）

    A、2个 B、3个 C、4个 D、5个

    查看试题解析

二、填空题

  • 9. 二次函数y＝x2﹣2x+3图象与y轴的交点坐标是.

    查看试题解析

  • 10. 将抛物线y=x2+1沿x轴向下翻折，则得到的新抛物线的解析式为 ．

    查看试题解析

  • 11. 若抛物线y=2(x−3)2−8与x轴的两个交点分别为点A和点B，则线段AB的长为 ．

    查看试题解析

  • 12. 如图是二次函数y=ax2+bx+c图象的一部分，对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c>0的解集是 ．

    查看试题解析

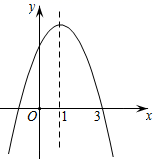  • 13. 如图（1）是一个横断面为抛物线形状的拱桥，水面在1时，拱顶(拱桥洞的最高点)离水面3米，水面宽4米．如果按图（2）建立平面直角坐标系，那么抛物线的解析式是 ．

    查看试题解析

  • 14. 如图，抛物线y＝﹣x2+4x﹣3与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1 ， 将C1向右平移得C2 ， C2与x轴交于点B，D.若直线y＝x+m与C1、C2共有3个不同的交点，则m的取值范围是.

    查看试题解析

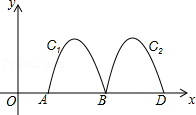  • 15. 如图，已知二次函数y＝ax2+bx+c（a＜0）的图象与x轴交于不同两点，与y轴的交点在y轴正半轴，它的对称轴为直线x＝1．有以下结论：①abc＞0，②a+c＞0，③若点（﹣1，y1）和（2，y2）在该图象上，则y1＜y2 ， ④设x1 ， x2是方程ax2+bx+c＝0的两根，若am2+bm+c＝p，则p（m﹣x1）（m﹣x2）≤0．其中正确的结论是（填入正确结论的序号）。

    查看试题解析

三、作图题

  • 16. 已知二次函数 y=(x+m)(x−1) 的图象经过点 (2 ， −3) .

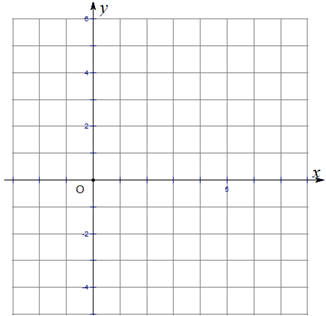    (1)、求这个二次函数的表达式；
    (2)、画出这个函数的图象，并利用图象解决下列问题：

    ①直接写出方程 (x+m)(x−1)=−3 的解；

    ②当x满足什么条件时， y>0 .

    查看试题解析

四、解答题

  • 17. 已知二次函数y＝x2﹣4x+c（c是常数）的图象与x轴只有一个交点，求c的值及这个交点的坐标．

    查看试题解析

  • 18.  已知二次函数y＝x2﹣mx+2m﹣4 

    证明：无论m取任何实数时，该函数图象与x轴总有交点

    查看试题解析

  • 19. 已知二次函数y＝x2+bx+c.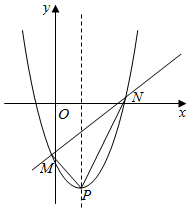

    (Ⅰ)若二次函数的图象经过(3，﹣2)，且对称轴为x＝1，求二次函数的解析式；

    (Ⅱ)如图，在(Ⅰ)的条件下，过定点的直线y＝﹣kx+k﹣4(k≤0)与(1)中的抛物线交于点M，N，且抛物线的顶点为P，若△PMN的面积等于3，求k的值；

    (Ⅲ)当c＝b2时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式.

    查看试题解析

五、综合题

  • 20. 某蛋糕店有线下和网上两种销售方式，每天共销售50个。已知线下和网上销售的纯利润分别为24元/个，20元/个，每天的总纯利润为1120元.
    (1)、求线下和网上的销售量分别是多少.
    (2)、该店为了扩大业务，增加了销售量。调查发现，线下销售的每个蛋糕的纯利润保持不变；网上销售在原来的基础上每降低1元的纯利润，销售量增加2个.

    ①该店当天线下和网上销售量均为34个，求当天的总纯利润？

    ②若线下增加的销售量不超过原来线下销售量的13 ， 该店每天生产多少个蛋糕，可使当天的总纯利润最大？

    查看试题解析

  • 21. 如图，直线y1=kx+b与函数y2=kx(x<0)的图象相交于点A(-1，6)，与x轴交于点C，且∠ACO=45°，点D是线段AC上一点.

    (1)、求k的值与一次函数的解析式.
    (2)、若直线与反比例函数的另一支交于B点，直接写出y1＜y2自变量x的取值范围，并求出△AOB的面积.
    (3)、若S△COD：S△AOC=2：3，求点D的坐标.

    查看试题解析