26.3 实践与探索----华师大版九年级下册同步试卷
试卷更新日期:2022-01-25 类型:同步测试
一、单选题
-
1. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0 的解集是( )
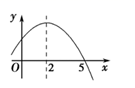 A、 B、 C、 或 D、 或2. 二次函数 的图象与x轴交点的个数为( )A、0个 B、1个 C、2个 D、1个或2个3. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+2.32=0的根是( )
A、 B、 C、 或 D、 或2. 二次函数 的图象与x轴交点的个数为( )A、0个 B、1个 C、2个 D、1个或2个3. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+2.32=0的根是( )x
……
0
4
……
y
……
0.32
﹣2
0.32
……
A、0或4 B、1或5 C、 或4﹣ D、 或 ﹣24. 如图,已知抛物线 与直线 交于 , 两点,则关于x的不等式 的解集是( )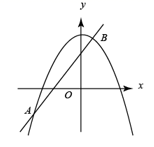 A、或 B、或 C、 D、5. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( )
A、或 B、或 C、 D、5. 将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为( ) A、或 B、或 C、或 D、或6. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元7. 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m , 则水面下降1m时,水面宽度增加( )
A、或 B、或 C、或 D、或6. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元7. 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m , 则水面下降1m时,水面宽度增加( ) A、1m B、2m C、(2 ﹣4)m D、( ﹣2)m8. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )
A、1m B、2m C、(2 ﹣4)m D、( ﹣2)m8. 学校卫生间的洗手盘台面上有一瓶洗手液(如图①).小丽经过测量发现:洗手液瓶子的截面图下部分是矩形CGHD,洗手液瓶子的底面直径GH=12cm,D,H与喷嘴位置点B三点共线.当小丽按住顶部A下压至如图②位置时,洗手液从喷口B流出(此时喷嘴位置点B距台面的距离为16cm),路线近似呈抛物线状,小丽在距离台面15cm处接洗手液时,手心Q到直线DH的水平距离为4cm,若小丽不去接,则洗手液落在台面的位置距DH的水平距离是16cm.根据小丽测量所得数据,可得洗手液喷出时的抛物线函数解析式的二次项系数是( )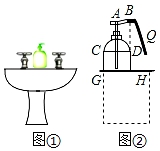 A、﹣ B、 C、﹣ D、9. 设 , 分别是函数 , 图象上的点,当 时,总有 恒成立,则称函数 , 在 上是“逼近函数”, 为“逼近区间”.则下列结论:
A、﹣ B、 C、﹣ D、9. 设 , 分别是函数 , 图象上的点,当 时,总有 恒成立,则称函数 , 在 上是“逼近函数”, 为“逼近区间”.则下列结论:①函数 , 在 上是“逼近函数”;②函数 , 在 上是“逼近函数”;③ 是函数 , 的“逼近区间”;④ 是函数 , 的“逼近区间”.其中,正确的有( )
A、②③ B、①④ C、①③ D、②④二、填空题
-
10. 抛物线与x轴正半轴交点的坐标为 .11. 如图,是二次函数y=ax2+bx﹣c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是 . (精确到0.1)
 12. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.
12. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m. 13. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,
13. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
 14. 图1是一个高脚杯截面图,杯体CBD呈抛物线状(杯体厚度不计),点B是抛物线的顶点,AB=9,EF=2 ,点A是EF的中点,当高脚杯中装满液体时,液面CD=4 ,此时最大深度(液面到最低点的距离)为10.以EF所在直线为x轴,AB所在直线为y轴建立平面直角坐标系,求抛物线的解析式 ;将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,此时杯体内液体的最大深度为 .
14. 图1是一个高脚杯截面图,杯体CBD呈抛物线状(杯体厚度不计),点B是抛物线的顶点,AB=9,EF=2 ,点A是EF的中点,当高脚杯中装满液体时,液面CD=4 ,此时最大深度(液面到最低点的距离)为10.以EF所在直线为x轴,AB所在直线为y轴建立平面直角坐标系,求抛物线的解析式 ;将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,此时杯体内液体的最大深度为 .
三、解答题
-
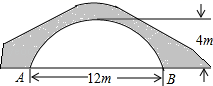
15. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费80元时,床位可全部租出,若每张床位每天收费提高10元,则相应的减少了10张床位租出,如果每张床位每天以10元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天应提高多少元?16. 如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,求选取点B为坐标原点时的抛物线解析式.
 17. 某幢建筑物,从5米高的窗口 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直,如图所示),如果抛物线的最高点 离墙1米,此时高度为10米.如图,在所示的平面直角坐标系中,求水流落地点 离墙距离 .(结果保留根号)
17. 某幢建筑物,从5米高的窗口 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直,如图所示),如果抛物线的最高点 离墙1米,此时高度为10米.如图,在所示的平面直角坐标系中,求水流落地点 离墙距离 .(结果保留根号)
四、综合题
-
18. 如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.

 (1)、分别求抛物线和直线AC的解析式;(2)、在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1 , 且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、分别求抛物线和直线AC的解析式;(2)、在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1 , 且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.