26.2.3 求二次函数的表达式----华师大版九年级下册同步试卷

试卷更新日期：2022-01-25 类型：同步测试

进入出卷网下载

一、单选题

1. 将二次函数y＝x²﹣2x﹣2化成顶点式，下列式子正确的是（）

A、y＝（x+1）²﹣1 B、y＝（x+1）²﹣3 C、y＝（x﹣1）²﹣1 D、y＝（x﹣1）²﹣3

查看试题解析
2. 若抛物线y＝x²+bx+c的对称轴为y轴，且点P（2，6）在该抛物线上，则c的值为（　　）

A、﹣2 B、0 C、2 D、4

查看试题解析
3. 如图，是一条抛物线的图象，则其解析式为（　　）

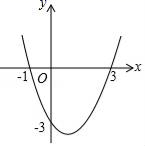A、y=x²﹣2x+3 B、y=x²﹣2x﹣3 C、y=x²+2x+3 D、y=x²+2x-3

查看试题解析
4. 已知二次函数 $y = a x^{2} + x + a (a - 2)$ 的图象经过原点，则a的值为（）

A、0或2 B、0 C、2 D、无法确定

查看试题解析
5. 已知关于x的抛物线y=x²-ax-4的对称轴为直线x=2，则下列各点在这条抛物线上的是（）

A、(3，4) B、(-2，-8) C、(4，4) D、( $- \frac{1}{2}$ ， $- \frac{7}{4}$ )

查看试题解析
6. 如图，一段抛物线：y=-x（x-3）（0≤x≤3），记为C₁ ，它与x轴交于点O ， A₁；将C₁绕点A₁旋转180°得C₂ ，交x轴于点A₂；将C₂绕点A₂旋转180°得C₃ ，交x轴于点A₃；…如此进行下去，直至得C₅ ．若P(14，m)在第5段抛物线C₅上，则m值为（）

A、2 B、1.5 C、-2 D、-2.25

查看试题解析
7. 已知二次函数y＝ax²+bx+c（a ， b ， c为常数，a≠0），其中，自变量x与函数值y之间满足下面对应关系：

x

……

$-$ 5

$-$ 3

$-$ 1

……

y＝ax²+bx+c

……

$-$ 2.5

1.5

1.5

……

则 $\frac{b (a + b + c)}{a}$ 的值是（　　）

A、﹣10 B、﹣5 C、﹣ $\frac{5}{2}$ D、﹣ $\frac{5}{4}$

查看试题解析
8. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ，且 $OB = OC = 3 OA = 3$ ，则下列结论：① $a b c > 0$ ；② $4 a c - b^{2} < 0$ ；③当 $- 2 \leq x \leq 2$ 时， $y$ 随 $x$ 的增大而增大；④将抛物线在 $y$ 轴左侧的部分沿过点 $C$ 且平行于 $x$ 轴的直线 $l$ 翻折，抛物线的其余部分保持不变得到一个新图象，当函数 $y = k$ （ $k$ 为常数）的图象与新图象有3个公共点时， $k$ 的取值范围是 $3 < k \leq 4$ ，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 请写出一个开口向下，并且与 $y$ 轴交于点 $(0 ， 4)$ 的抛物线的解析式．

查看试题解析
10. 二次函数 $y = (m + 3) x^{2} + 3 x + m^{2} - 9$ 的图象经过原点，则 $m =$ ．

查看试题解析
11. 如图，已知二次函数 y=ax²+bx+c 的图象与 x 轴交于 A（1，0），B（3，0）两点，与 y 轴交于点 C（0，3），则二次函数的图象的顶点坐标是．

查看试题解析
12. 已知二次函数 $y = a x^{2} + b x + c$ （ $a ， b ， c$ 是常数， $a \neq 0$ ）的y与x的部分对应值如下表：
$x$
$- 5$
$- 4$
$- 2$
0
2
$y$
6
0
$- 6$
$- 4$
6
下列结论：
① $a > 0$ ；
②当 $x = - 2$ 时，函数最小值为 $- 6$ ；
③若点 $(- 8 ， y_{1})$ ，点 $(8 ， y_{2})$ 在二次函数图象上，则 $y_{1} < y_{2}$ ；
④方程 $a x^{2} + b x + c = - 5$ 有两个不相等的实数根．
其中，正确结论的序号是．（把所有正确结论的序号都填上）

查看试题解析

三、解答题

13. 已知二次函数y＝（m²﹣2）x²﹣4mx+n的图象的对称轴是直线x＝2，且最高点在直线y＝ $\frac{1}{2}$ x+1上，求这个二次函数的表达式．

查看试题解析
14. 如图，已知：关于y的二次函数 $y = x^{2} + b x + c$ 的图象与x轴交于点 $A (2 ， 0)$ 和点B，与y轴交于点 $C (0 ， 6)$ ，抛物线的对称轴与x轴交于点D.

(1)、求二次函数的表达式.

(2)、在y轴上是否存在一点P，使 $△ P B C$ 为直角三角形.若存在，请求出点P的坐标.

(3)、有一个点M从点A出发，以每秒1个单位的速度在 $A B$ 上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达B点时，点M、N同时停止运动，问点M、N运动到何处时， $△ M N B$ 面积最大，试求出面积.

查看试题解析

x	……	$-$ 5	$-$ 3	$-$ 1	……
y＝ax²+bx+c	……	$-$ 2.5	1.5	1.5	……

$x$	$- 5$	$- 4$	$- 2$	0	2
$y$	6	0	$- 6$	$- 4$	6