湖北省鄂州市鄂城区2021-2022学年九年级上学期期末数学试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 关于x的一元二次方程 的一个根是3,则m的值是( )A、3 B、 C、9 D、2. 抛物线 的对称轴是直线( )A、 B、 C、 D、3. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、 B、 C、 D、4. 不透明袋中装有3个红球和5个绿球,这些球除颜色外无其他差别.从袋中随机摸出1个球是红球的概率为( )A、 B、 C、 D、5. 已知反比例函数的图象经过点 ,则这个反比例函数的解析式为( )A、 B、 C、 D、6. 下列说法正确的个数有( )
①方程 的两个实数根的和等于1;
②半圆是弧;
③正八边形是中心对称图形;
④“抛掷3枚质地均匀的硬币全部正面朝上”是随机事件;
⑤如果反比例函数的图象经过点 ,则这个函数图象位于第二、四象限.
A、2个 B、3个 C、4个 D、5个7. 如图, 中的半径为1, 内接于 .若 , ,则 的长是( ) A、 B、 C、 D、8. 如图,抛物线 的对称轴是直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( )
A、 B、 C、 D、8. 如图,抛物线 的对称轴是直线 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( )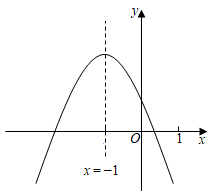 A、1个 B、2个 C、3个 D、4个9. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、1个 B、2个 C、3个 D、4个9. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )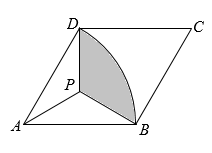 A、 B、 C、 D、10. 如图, 中, , ,点D是边 上一动点,连接 ,以 为直径的圆交 于点E.若 长为4,则线段 长的最小值为( )
A、 B、 C、 D、10. 如图, 中, , ,点D是边 上一动点,连接 ,以 为直径的圆交 于点E.若 长为4,则线段 长的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则关于x的一元二次方程 必有一个根为.12. 若抛物线y=x2﹣6x+m与x轴有两个公共点,则m的取值范围是 .13. 飞机着陆后滑行的距离s(单位:m)关于滑行的时间t(单位:s)的函数解析式是s=60t﹣12t2.飞机着陆后滑行 米才能停下来.14. 圆锥底面圆的半径为2cm,其侧面展开图的圆心角是180°,则圆锥的侧面积是 .15. 如图,已知 的半径为1,圆心P在抛物线 上运动,当 与x轴相切时,圆心P的横坐标为.
 16. 如图,已知 , 是反比例函数 图象上的两点,动点 在x轴正半轴上运动,当 达到最大时,点P的坐标是.
16. 如图,已知 , 是反比例函数 图象上的两点,动点 在x轴正半轴上运动,当 达到最大时,点P的坐标是.
三、解答题
-
17. 解下列方程:(1)、 ;(2)、 .18. 如图,在 的方格纸中, 的三个顶点都在格点上,我们把这样的三角形叫做格点三角形(每个小方格都是边长为1个单位长度的正方形).请完成以下画图并填空.
 (1)、在图1中画出一个与 成中心对称的格点三角形;(2)、在图2中画出一个与 成轴对称且与 有公共边的格点三角形;(3)、在图3中画出将 绕点C顺时针旋转 后得到的三角形,其中顶点A在旋转过程中经过的路径长为.(直接填结果)19. 落实“双减”政策,丰富课后服务,为了发展学生兴趣特长,梁鄂中学七年级准备开设A(窗花剪纸)、B(书法绘画)、C(中华武术)、D(校园舞蹈)四门选修课程(每位学生必须且只选其中一门),甲、乙两位同学分别随机选择其中一门选修课程参加学习.用列表法或画树状图法求:(1)、甲、乙都选择A(窗花剪纸)课程的概率;(2)、甲、乙选择同一门课程的概率.20. 设 , 是关于x的一元二次方程 的两个实数根.(1)、求m的取值范围;(2)、若 ,求m的值.21. 学习完二次函数后,某班“数学兴趣小组”的同学对函数 的图象和性质进行了探究.在经历列表、描点、连线步骤后得到其图象如图所示.请根据函数图象完成以下问题:
(1)、在图1中画出一个与 成中心对称的格点三角形;(2)、在图2中画出一个与 成轴对称且与 有公共边的格点三角形;(3)、在图3中画出将 绕点C顺时针旋转 后得到的三角形,其中顶点A在旋转过程中经过的路径长为.(直接填结果)19. 落实“双减”政策,丰富课后服务,为了发展学生兴趣特长,梁鄂中学七年级准备开设A(窗花剪纸)、B(书法绘画)、C(中华武术)、D(校园舞蹈)四门选修课程(每位学生必须且只选其中一门),甲、乙两位同学分别随机选择其中一门选修课程参加学习.用列表法或画树状图法求:(1)、甲、乙都选择A(窗花剪纸)课程的概率;(2)、甲、乙选择同一门课程的概率.20. 设 , 是关于x的一元二次方程 的两个实数根.(1)、求m的取值范围;(2)、若 ,求m的值.21. 学习完二次函数后,某班“数学兴趣小组”的同学对函数 的图象和性质进行了探究.在经历列表、描点、连线步骤后得到其图象如图所示.请根据函数图象完成以下问题: (1)、观察发现:
(1)、观察发现:①写出该函数的一条性质;
②函数图象与x轴有个交点,所以对应的方程 有个实数根;
(2)、分析思考:③方程 的解为;
④关于 的方程 有4个实数根时,m的取值范围是;
(3)、延伸探究:⑤将函数 的图象经过怎样的平移可以得到函数 的图象,直接写出平移过程.
22. 如图, 是 的直径,弦 ,E是 的中点,连接 并延长到点F,使 ,连接 交 于点D,连接 , . (1)、求证:直线 是 的切线;(2)、若 长为 ,求 的半径及 的长.23. 绿色生态农场生产并销售某种有机生态水果.经市场调查发现,该生态水果的周销售量y(千克)是销售单价x(元/千克)的一次函数.其销售单价、周销售量及周销售利润w(元)的对应值如表.请根据相关信息,解答下列问题:
(1)、求证:直线 是 的切线;(2)、若 长为 ,求 的半径及 的长.23. 绿色生态农场生产并销售某种有机生态水果.经市场调查发现,该生态水果的周销售量y(千克)是销售单价x(元/千克)的一次函数.其销售单价、周销售量及周销售利润w(元)的对应值如表.请根据相关信息,解答下列问题:销售单价x(元/千克)
40
50
周销售量y(千克)
180
160
周销售利润w(元)
1800
3200
(1)、这种有机生态水果的成本为元/千克;(2)、求该生态水果的周销售量y(千克)与销售单价x(元/千克)之间的函数关系式;(3)、若农场按销售单价不低于成本价,且不高于60元/千克销售,则销售单价定为多少,才能使销售该生态水果每周获得的利润w(元)最大?最大利润是多少?24. 如图1,在平面直角坐标系 中,抛物线 经过点 ,且与直线 在第二象限交于点A,过点A作 轴,垂足为点 .若P是直线 上方该抛物线上的一个动点,过点P作 轴于点C,交 于点D,连接 , . (1)、求抛物线的解析式;(2)、求 的面积S的最大值;(3)、连接 交 于点E,如图2,线段 与 能否互相平分?若能,请求出点E的坐标;若不能,请说明理由.
(1)、求抛物线的解析式;(2)、求 的面积S的最大值;(3)、连接 交 于点E,如图2,线段 与 能否互相平分?若能,请求出点E的坐标;若不能,请说明理由.